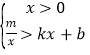ћвƒњƒЏ»Ё
°Њћвƒњ°њ‘ƒґЅ≤ƒЅѕ£Ї
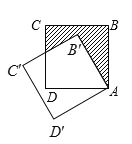
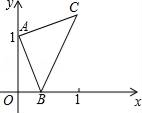
ќ“√«÷™µј£Ї“їћх÷±ѕяЊ≠єэµ»—ь÷±љ«»эљ«–ќµƒ÷±љ«ґ•µг£ђєэЅнЌвЅљЄцґ•µгЈ÷±рѕтЄ√÷±ѕя„чієѕя£ђЉіњ…µ√»эіє÷±ƒ£–Ќ°±»зЌЉҐў£ђ‘Џ![]() ÷–£ђ
÷–£ђ![]() £ђ
£ђ![]() £ђЈ÷±рєэ
£ђЈ÷±рєэ![]() °Ґ
°Ґ![]() ѕтЊ≠єэµг
ѕтЊ≠єэµг![]() ÷±ѕя„чієѕя£ђіє„гЈ÷±рќ™
÷±ѕя„чієѕя£ђіє„гЈ÷±рќ™![]() °Ґ
°Ґ![]() £ђќ“√«Ї№»Ё“„ЈҐѕ÷љб¬џ£Ї
£ђќ“√«Ї№»Ё“„ЈҐѕ÷љб¬џ£Ї![]() £Ѓ
£Ѓ

£®1£©ћљЊњќ ћв£Ї»зєы![]() £ђ∆дЋыћхЉю≤ї±д£ђ»зЌЉҐЏ£ђњ…µ√µљљб¬џ£ї
£ђ∆дЋыћхЉю≤ї±д£ђ»зЌЉҐЏ£ђњ…µ√µљљб¬џ£ї![]() £Ѓ«лƒгЋµ√чјн”…£Ѓ
£Ѓ«лƒгЋµ√чјн”…£Ѓ
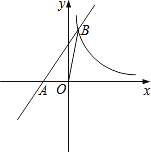
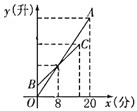
£®2£©—І“‘÷¬”√£Ї»зЌЉҐџ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђ÷±ѕя![]() ”л÷±ѕя
”л÷±ѕя![]() љї”Џµг
љї”Џµг![]() £ђ«“Ѕљ÷±ѕяЉ–љ«ќ™
£ђ«“Ѕљ÷±ѕяЉ–љ«ќ™![]() £ђ«“
£ђ«“![]() £ђ«лƒг«у≥ц÷±ѕя
£ђ«лƒг«у≥ц÷±ѕя![]() µƒљвќц љ£Ѓ
µƒљвќц љ£Ѓ
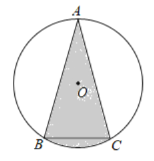
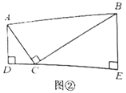
£®3£©ЌЎ’є”¶”√£Ї»зЌЉҐ№£ђ‘ЏЊЎ–ќ![]() ÷–£ђ
÷–£ђ![]() £ђ
£ђ![]() £ђµг
£ђµг![]() ќ™
ќ™![]() ±я…ѕ°™Єцґѓµг£ђЅђљ”
±я…ѕ°™Єцґѓµг£ђЅђљ”![]() £ђљЂѕяґќ
£ђљЂѕяґќ![]() »∆µг
»∆µг![]() Ћ≥ ±’л–э„™
Ћ≥ ±’л–э„™![]() £ђµг
£ђµг![]() ¬д‘Џµг
¬д‘Џµг![]() і¶£ђµ±µг
і¶£ђµ±µг![]() ‘ЏЊЎ–ќ
‘ЏЊЎ–ќ![]() Ќв≤њ ±£ђЅђљ”
Ќв≤њ ±£ђЅђљ”![]() £ђ
£ђ![]() £Ѓ»ф
£Ѓ»ф![]() ќ™÷±љ«»эљ«–ќ ±£ђ«лƒгћљЊњ≤Ґ÷±љ”–і≥ц
ќ™÷±љ«»эљ«–ќ ±£ђ«лƒгћљЊњ≤Ґ÷±љ”–і≥ц![]() µƒ≥§£Ѓ
µƒ≥§£Ѓ
°Њір∞Є°њ£®1£©јн”…Љыљвќц£ї£®2£©![]() £ї£®3£©
£ї£®3£©![]() ≥§ќ™3їт
≥§ќ™3їт![]() £Ѓ
£Ѓ
°Њљвќц°њ
£®1£©ЄщЊЁЌђљ«µƒ”аљ«ѕаµ»µ√µљ![]() £ђ»їЇујы”√AAґ®јн≈–ґ®»эљ«–ќѕаЋ∆£ї
£ђ»їЇујы”√AAґ®јн≈–ґ®»эљ«–ќѕаЋ∆£ї
£®2£©єэµг![]() „ч
„ч![]() љї÷±ѕя
љї÷±ѕя![]() ”Џµг
”Џµг![]() £ђЈ÷±рєэ
£ђЈ÷±рєэ![]() °Ґ
°Ґ![]() „ч
„ч![]() ÷б£ђ
÷б£ђ![]() ÷б£ђ”…£®1£©µ√
÷б£ђ”…£®1£©µ√![]() £ђі”ґшµ√µљ
£ђі”ґшµ√µљ![]() £ђ»їЇуљбЇѕѕаЋ∆»эљ«–ќµƒ–‘÷ ЇЌ»сљ«»эљ«Їѓ э«у≥ц
£ђ»їЇуљбЇѕѕаЋ∆»эљ«–ќµƒ–‘÷ ЇЌ»сљ«»эљ«Їѓ э«у≥ц![]() £ђ
£ђ![]() £ђі”ґш»Јґ®Nµг„ш±к£ђ»їЇујы”√іэґ®ѕµ эЈ®«уЇѓ эљвќц љ£ї
£ђі”ґш»Јґ®Nµг„ш±к£ђ»їЇујы”√іэґ®ѕµ эЈ®«уЇѓ эљвќц љ£ї
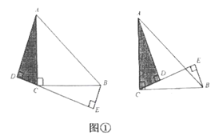
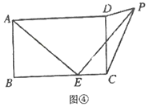
£®3£©Ј÷Ѕљ÷÷«й–ќћ÷¬џ£ЇҐў»зЌЉ1÷–£ђµ±°ѕPDC=90°г ±£ЃҐЏ»зЌЉ2÷–£ђµ±°ѕDPC=90°г ±£ђ„чPF°ЌBC”ЏF£ђPH°ЌCD”ЏH£ђ…иBE=x£ЃЈ÷±р«уљвЉіњ…£Ѓ
љв£Ї£®1£©°я![]() £ђ°а
£ђ°а![]()
”÷°я![]()
°а![]()
°а![]()
°я![]() £Ѓ
£Ѓ
°а![]()
£®2£©»зЌЉ£ђєэµг![]() „ч
„ч![]() љї÷±ѕя
љї÷±ѕя![]() ”Џµг
”Џµг![]() £ђ
£ђ
Ј÷±рєэ![]() °Ґ
°Ґ![]() „ч
„ч![]() ÷б£ђ
÷б£ђ![]() ÷б
÷б
”…£®1£©µ√![]() °а
°а![]()
°я![]() „ш±к
„ш±к![]() °а
°а![]() £ђ
£ђ![]()
°я![]() °а
°а![]()
љвµ√£Ї![]() £ђ
£ђ![]() °а
°а![]()
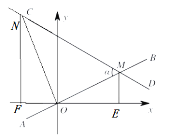
…и÷±ѕя![]() ±ніп љќ™
±ніп љќ™![]() £ђіъ»л
£ђіъ»л![]() £ђ
£ђ![]()
µ√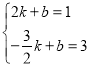 £ђљвµ√
£ђљвµ√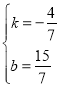 £ђ
£ђ
°а÷±ѕя![]() ±ніп љќ™
±ніп љќ™![]()
£®3£©љв£ЇҐў»зЌЉ1÷–£ђµ±°ѕPDC=90°г ±£ђ
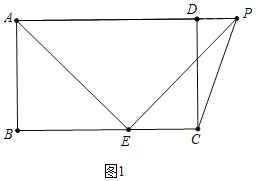
°я°ѕADC=90°г£ђ
°а°ѕADC+°ѕPDC=180°г£ђ
°аA°ҐD°ҐPє≤ѕя£ђ
°яEA=EP£ђ°ѕAEP=90°г£ђ
°а°ѕEAP=45°г£ђ°я°ѕBAD=90°г£ђ
°а°ѕBAE=45°г£ђ°я°ѕB=90°г
°а°ѕBAE=°ѕBEA=45°г£ђ
°аBE=AB=3£Ѓ
ҐЏ»зЌЉ2÷–£ђµ±°ѕDPC=90°г ±£ђ„чPF°ЌBC”ЏF£ђPH°ЌCD”ЏH£ђ…иBE=x£ђ
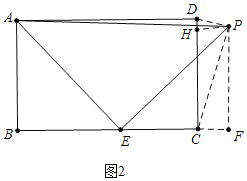
°я°ѕAEB+°ѕPEF=90°г£ђ°ѕAEB+°ѕBAE=90°г£ђ
°а°ѕBAE=°ѕPEF£ђ
‘Џ°чABEЇЌ°чEFP÷–£ђ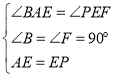
°а°чABE°’°чEFP£ђ
°аEF=AB=3£ђPF=HC=BE=x£ђ
°аCF=3-£®5-x£©=x-2£ђ
°я°ѕDPH+°ѕCPH=90°г£ђ°ѕCPH+°ѕPCH=90°г£ђ
°а°ѕDPH=°ѕPCH£ђ°я°ѕDHP=°ѕPHC£ђ
°а°чPHD°„°чCHP£ђ
°аPH2=DHCH£ђ
°а£®x-2£©2=x£®3-x£©£ђ
°аx=![]() їт
їт![]() £®…б∆ъ£©£ђ
£®…б∆ъ£©£ђ
°аBE=![]() £ђ
£ђ
„џ…ѕЋщ ц£ђµ±°чPDC «÷±љ«»эљ«–ќ ±£ђBEµƒ÷µќ™3їт![]() £Ѓ
£Ѓ