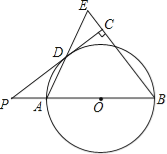
题目内容
【题目】已知直线![]() ,抛物线
,抛物线![]() .
.
![]() 当
当![]() ,
,![]() 时,求直线
时,求直线![]() 与抛物线
与抛物线![]() 的交点坐标;
的交点坐标;
![]() 当
当![]() ,
,![]() 时,将直线
时,将直线![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 后与抛物线
后与抛物线![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),求
点的左侧),求![]() ,
,![]() 两点的坐标;
两点的坐标;
![]() 若将
若将![]() 中的条件“
中的条件“![]() ”去掉,其他条件不变,且
”去掉,其他条件不变,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1) 直线![]() 与抛物线
与抛物线![]() 的交点坐标是
的交点坐标是![]() 或
或![]() ;(2)
;(2) ![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)联立方程,解方程求得即可;
(2)由题意得旋转后的直线的解析式为y=![]() x,然后联立方程,解方程求得即可;
x,然后联立方程,解方程求得即可;
(3)根据题意求得交点坐标,然后根据勾股定理表示出AB,得出不等式,解不等式即可求得c的取值范围.
![]() ∵
∵![]() ,
,![]() ,
,
∴抛物线![]() .
.
解![]() 得
得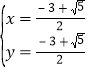 或
或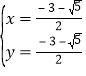 ,
,
∴直线![]() 与抛物线
与抛物线![]() 的交点坐标是
的交点坐标是![]() 或
或![]() ;
;
![]() 设直线绕原点逆时针旋转
设直线绕原点逆时针旋转![]() 得到直线
得到直线![]() ,
,
而直线![]() 与
与![]() 轴的夹角为
轴的夹角为![]() ,
,
∴旋转后直线![]() 与
与![]() 轴的夹角为
轴的夹角为![]() ,
,
∴旋转后的直线![]() 的解析式为
的解析式为![]() ,
,
解![]() 得
得![]() 或
或![]() ,
,
∴![]() ,
,![]() ;
;
![]() 若将
若将![]() 中的条件“
中的条件“![]() ”去掉,其他条件不变,
”去掉,其他条件不变,
∵![]() ,
,
∴抛物线的对称轴为![]() ,
,
代入![]() 得,
得,![]() ,
,
∵抛物线![]() 与直线
与直线![]() 有交点,
有交点,
∴抛物线的顶点在![]() 下,
下,
∴![]() ,即
,即![]() ,
,
解得![]() .
.

练习册系列答案
相关题目