题目内容
数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离，他们设计了如图所示的测量方案：从树A沿着垂直于AB的方向走到E，再从E沿着垂直于AE的方向走到F，C为AE上一点，其中3位同学分别测得三组数据：①AC，∠ACB；②EF、DE、AD；③CD，∠ACB，∠ADB．其中能根据所测数据求得A、B两树距离的有（ ）| A、0组 | B、一组 | C、二组 | D、三组 |
分析：根据三角形相似可知，要求出AB，只需求出EF即可．所以借助于（1）（3），根据AB=
即可解答．
| EF•AC |
| CE |
解答：解：此题比较综合，要多方面考虑，
第①组中，因为知道∠ACB和AC的长，所以可利用∠ACB的正切来求AB的长；
第②组中可利用∠ACB和∠ADB的正切求出AB；
第③组中设AC=x，AD=CD+x，AB=
，AB=
；因为已知CD，∠ACB，∠ADB，可求出x，然后得出AB．
故选D．
第①组中，因为知道∠ACB和AC的长，所以可利用∠ACB的正切来求AB的长；
第②组中可利用∠ACB和∠ADB的正切求出AB；
第③组中设AC=x，AD=CD+x，AB=
| x |
| tan∠ACB |
| x+CD |
| tan∠ADB |
故选D．
点评：本题考查解直角三角形的应用，解答道题的关键是将实际问题转化为数学问题，本题只要把实际问题抽象到相似三角形，解直角三角形即可求出．
练习册系列答案
相关题目
为测量被池塘相隔的两棵树A，B的距离，数学课外兴趣小组的同学们设计了如图所示的测量方案：从树A沿着垂直于AB的方向走到E，再从E沿着垂直于AE的方向走到F，C为AE上一点，其中3位同学分别测得三组数据：（1）AC，∠ACB（2）CD，∠ACB，∠ADB（3）EF，DE，AD，其中能根据所测数据求得A，B两树距离的有（ ）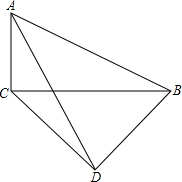
我市某校初三年级数学课外兴趣小组的同学们对手上的两块三角板进行了探索，他们发现：将两块三角板按如图放置，连接AD，能确定cot∠CAD的值，你认为cot∠CAD=
