Question

【题目】如图1，已知△ABC和△EFC都是等边三角形，且点E在线段AB上．

（1）求证：BF∥AC；

（2）过点E作EG∥BC交AC于点G，试判断△AEG的形状并说明理由；

（3）如图2，若点D在射线CA上，且ED＝EC，求证：AB＝AD＋BF．

Answer 1

【答案】（1）见解析；（2）△AEG是等边三角形；理由见解析；（3）见解析.

【解析】

（1）如图1，根据等边三角形的性质得到∠ACB=∠ECF=60°，AC=BC，CE=FC，推出△ACE≌△FCB，得到∠CBF=∠A=60°，于是得到∠CBF =∠ACB，根据平行线的判定定理即可得到AC∥BF；
（2）过E作EG∥BC交AC于G，根据等边三角形的判定定理可证明△AEG是等边三角形；

（3）由（2）可知∠DAE=∠EGC=120°，可证明△ADE≌△GCE，进而得到AD=CG，再由（1）BF=AE=AG，于是可证得AB=BF+AD.

解：（1）如图1，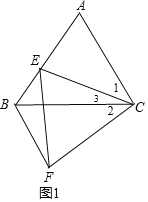

∵△ABC和△EFC都是等边三角形，
∴∠ACB=∠ECF=∠A= 60°，AC=BC，CE=FC，
∴∠1+∠3=∠2+∠3，
∴∠1=∠2，
在△ACE与△FCB中，

,

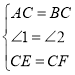∴△ACE≌△FCB，
∴∠CBF=∠A =60°，
∴∠CBF =∠ACB，

∴AC∥BF；
（2）△AEG是等边三角形，理由如下：

如图，过E作EG∥BC交AC于G，

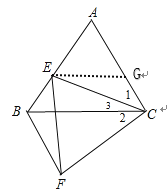
∵∠ABC=∠ACB=60°，
∴∠AEG=∠AGE=60°，
∴△AEG是等边三角形.
（3）如图2，过E作EG∥BC交AC于G，

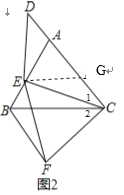
由（2）可知△AEG是等边三角形，

∴AE=EG=AG，∠GAE=∠AGC=60°，
∴∠DAE=∠EGC=120°，
∵DE=CE，

∴∠D=∠1，
∴△ADE≌△GCE，
∴AD=CG，
∴AC=AG+CG=AG+AD，

由（1）得△ACE≌△FCB，
∴BF=AE，
∴BF=AG，
∴AC=BF+AD，
∴AB=BF+AD.