Question

【题目】如图，直线与反比例函数在第一象限内的图象交于、两点，且与轴的正半轴交于点．若，的面积为，则的值为（ ）

A. 6 B. 9 C. 12 D. 18

Answer 1

【答案】A

【解析】

作AD⊥x轴于D，BE⊥x轴于E，先证明△CBE∽△CAD，利用相似比得到AD=3BE，设B（t，），利用反比例函数图象上点的坐标特征得到A点坐标为（t，），根据反比例函数的比例系数的几何意义得S△AOD=S△BOE，由于S△AOD+S梯形ABED=S△AOB+S△BOE，所以S△AOB=S梯形ABED，然后利用梯形的面积公式计算即可求得．

作AD⊥x轴于D,BE⊥x轴于E,如图,

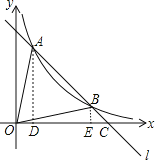
∵BE∥AD，

∴△CBE∽△CAD，

∴=，

∵AB=2BC，

∴CB:CA=1:3，

∴==，

∴AD=3BE，

设B(t,),则A点坐标为(t,)，

∵S△AOD+S梯形ABED=S△AOB+S△BOE，

而S△AOD=S△BOE,= k，

∴S△AOB=S梯形ABED= (+)(tt)=8，

解得k=6.

故答案选A.