题目内容
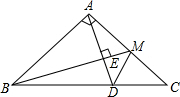 已知∠BAC=90°,AB=AC,M是AC边的中点,AD⊥BM交BC于D,交BM于E,
已知∠BAC=90°,AB=AC,M是AC边的中点,AD⊥BM交BC于D,交BM于E,求证:∠AMB=∠DMC.
分析:先延长AD至F,使得CF⊥AC,得出∠ABM=∠DAC,再根据AB=AC,CF⊥AC,得出△ABM≌△CAF,从而证出∠BMA=∠F,AM=CF,再根据所给的条件得出△FCD≌△MCD,即可得出∠AMB=∠F=∠CMD.
解答: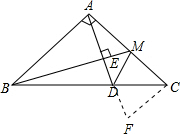 证明:如图,延长AD至F,使得CF⊥AC.
证明:如图,延长AD至F,使得CF⊥AC.
∵AB⊥AC,AD⊥BM,
∴∠ABM=∠DAC,
在△ABM与△CAF中,
,
∴△ABM≌△CAF(ASA),
∴∠BMA=∠F,AM=CF,
在△FCD与△MCD中,
,
∴△FCD≌△MCD(SAS),
∴∠F=∠CMD,
∴∠AMB=∠DMC.
 证明:如图,延长AD至F,使得CF⊥AC.
证明:如图,延长AD至F,使得CF⊥AC.∵AB⊥AC,AD⊥BM,
∴∠ABM=∠DAC,
在△ABM与△CAF中,
|
∴△ABM≌△CAF(ASA),
∴∠BMA=∠F,AM=CF,
在△FCD与△MCD中,
|
∴△FCD≌△MCD(SAS),
∴∠F=∠CMD,
∴∠AMB=∠DMC.
点评:此题考查了解等腰直角三角形;解题的关键是根据题意画出图形,再根据解等腰直角三角形的性质和全等三角形的判断与性质进行解答即可.

练习册系列答案
相关题目
 如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.
如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.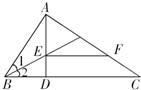 25、如图,已知∠BAC=90°,AD⊥BC于点D,∠1=∠2,EF∥BC交AC于点F.试说明AE=CF.
25、如图,已知∠BAC=90°,AD⊥BC于点D,∠1=∠2,EF∥BC交AC于点F.试说明AE=CF.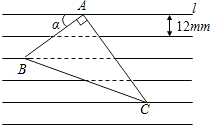 如图,把一张直角三角形卡片ABC放在每格宽度为12mm的横格纸中,三个顶点恰好都落在横格线上,已知∠BAC=90°,∠α=36°,求直角三角形卡片ABC的面积(精确到1mm).(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
如图,把一张直角三角形卡片ABC放在每格宽度为12mm的横格纸中,三个顶点恰好都落在横格线上,已知∠BAC=90°,∠α=36°,求直角三角形卡片ABC的面积(精确到1mm).(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)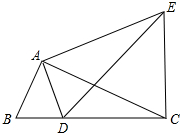 如图,已知∠BAC=90°,△ABC绕点A逆时针旋转得到△ADE,恰好D在BC上,连接CE.
如图,已知∠BAC=90°,△ABC绕点A逆时针旋转得到△ADE,恰好D在BC上,连接CE.