Question

20．如图，某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上，已知此人的眼睛到地面的距离AB=1.6m，标杆FC=2.2m，且BC=1m，CD=5m，标杆FC、ED垂直于地面．求电视塔的高ED．

Answer 1

分析 作AH⊥ED交FC于点G；把实际问题抽象到相似三角形中，利用相似三角形的对应边成比例列出方程，解方程即可．

解答 解：作AH⊥ED交FC于点G；如图所示：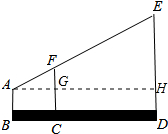                             
∵FC⊥BD，ED⊥BD，AH⊥ED交FC于点G，
∴FG∥EH，
∵AH⊥ED，BD⊥ED，AB⊥BC，ED⊥BC，
∴AH=BD，AG=BC，
∵AB=1.6，FC=2.2，BC=1，CD=5，
∴FG=2.2-1.6=0.6，BD=6，
∵FG∥EH，
∴$\frac{FG}{EH}=\frac{AG}{AH}，\frac{0.6}{EH}=\frac{1}{6}$，
解得：EH=3.6，
∴ED=3.6+1.6=5.2（m）
答：电视塔的高ED是5.2米．

点评 本题考查了相似三角形的应用；通过构造相似三角形．利用相似三角形对应边成比例是解决问题的关键．