题目内容
完成下面证明过程并写出推理根据：
已知：如图所示，∠BAP与∠APD互补，∠1＝∠2．
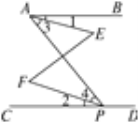
求证：∠E＝∠F．
证明：
∵∠BAP与∠APD互补(已知)，即∠BAP+∠APD=180°，
∴ ∥ ( )，
∴∠BAP＝∠APC ( )．
又∵∠1＝∠2，
∴∠BAP－∠1＝∠APC－∠2((等式的性质)，
即∠3＝∠4，
∴ ∥ ( )，
∴∠E＝∠F( )．
练习册系列答案
轻松暑假总复习系列答案
相关题目
轻松暑假总复习系列答案题目内容
完成下面证明过程并写出推理根据：
已知：如图所示，∠BAP与∠APD互补，∠1＝∠2．
求证：∠E＝∠F．
证明：
∵∠BAP与∠APD互补(已知)，即∠BAP+∠APD=180°，
∴ ∥ ( )，
∴∠BAP＝∠APC ( )．
又∵∠1＝∠2，
∴∠BAP－∠1＝∠APC－∠2((等式的性质)，
即∠3＝∠4，
∴ ∥ ( )，
∴∠E＝∠F( )．
轻松暑假总复习系列答案
，
得到
B. 
C. 
D. 
并把解集在给定的数轴上表示出来．
