题目内容
 如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P为线段BC上的点.小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标(3,4),请你写出其余所有符合这个条件的P点坐标
如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P为线段BC上的点.小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标(3,4),请你写出其余所有符合这个条件的P点坐标考点:矩形的性质,坐标与图形性质,等腰三角形的判定
专题:分类讨论
分析:根据点A、C的坐标求出OA、OC,再根据线段中点的定义求出OD=5,过点P作PE⊥x轴于E,根据已知点P(3,4)判断出OP=OD,再根据PD=OD利用勾股定理列式求出DE的长,然后分点E在点D的左边与右边两种情况求出OE,然后写出点P的坐标即可.
解答: 解:∵A(10,0),C(0,4),
解:∵A(10,0),C(0,4),
∴OA=10,OC=4,
∵点D是OA的中点,
∴OD=
OA=
×10=5,
过点P作PE⊥x轴于E,
则PE=OC=4,
∵P(3,4),
∴OP=
=5,
∴此时,OP=OD,
当PD=OD时,由勾股定理得,DE=
=
=3,
若点E在点D的左边,OE=5-3=2,
此时,点P的坐标为(2,4),
若点E在点D的右边,则OE=5+3=8,
此时,点P的组别为(8,4),
综上所述,其余的点P的坐标为(2,4)或(8,4).
故答案为:(2,4)或(8,4).
 解:∵A(10,0),C(0,4),
解:∵A(10,0),C(0,4),∴OA=10,OC=4,
∵点D是OA的中点,
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
过点P作PE⊥x轴于E,
则PE=OC=4,
∵P(3,4),
∴OP=
| 32+42 |
∴此时,OP=OD,
当PD=OD时,由勾股定理得,DE=
| PD2-PE2 |
| 52-42 |
若点E在点D的左边,OE=5-3=2,
此时,点P的坐标为(2,4),
若点E在点D的右边,则OE=5+3=8,
此时,点P的组别为(8,4),
综上所述,其余的点P的坐标为(2,4)或(8,4).
故答案为:(2,4)或(8,4).
点评:本题考查了矩形的性质,坐标与图形性质,等腰三角形的性质,勾股定理,难点在于要分两种情况写出点P的坐标.

练习册系列答案
相关题目
 如图,在直角坐标系中,四边形ABCO是正方形,已知点C的坐标为(
如图,在直角坐标系中,四边形ABCO是正方形,已知点C的坐标为(
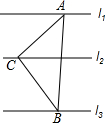 如图,已知△ABC中,∠ACB=90°,AC=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2与l3之间的距离为3,则△ABC的面积是
如图,已知△ABC中,∠ACB=90°,AC=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2与l3之间的距离为3,则△ABC的面积是