题目内容
 如图,已知等腰梯形ABCD的周长是20,AD∥BC,AD<BC,∠BAD=120°,对角线AC平分∠BCD,则S梯形ABCD=________.
如图,已知等腰梯形ABCD的周长是20,AD∥BC,AD<BC,∠BAD=120°,对角线AC平分∠BCD,则S梯形ABCD=________.
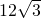
分析:根据题意可知,△ABF为等边三角形,则AD=CD=AB,即可求出AE=
 ,S梯形ABCD=12
,S梯形ABCD=12 .
.解答:
 解:如图:做AE垂直BC交BC于点E,做AF∥CD交BC于点F.
解:如图:做AE垂直BC交BC于点E,做AF∥CD交BC于点F.∵∠BAD=120°
∴∠B=60°
∵对角线AC平分∠BCD,
∴∠ACB=∠DCA=30°,
又∵AD∥BC,AF∥CD
∴∠DAC=∠DCA=30°,四边形ADCF为平行四边形
∴AD=AF=CD.
又∵AB=CD=AF
∴∠B=∠AFE=60°
∴△ABF为等边三角形
∵等腰梯形ABCD的周长是20
∴AD=CD=AB=4.BC=8
AE=
 =
=
故等腰梯形的面积为(AD+BC)×
 =12
=12
点评:本题要依靠辅助线的帮助,考查了等腰梯形的性质以及面积公式的有关知识.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 ,
, 3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( )
3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( ) 如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=
如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC= 13、如图,已知等腰梯形ABCD,AD∥BC,AD=5cm,BC=11cm,高DE=4cm,则梯形的周长为
13、如图,已知等腰梯形ABCD,AD∥BC,AD=5cm,BC=11cm,高DE=4cm,则梯形的周长为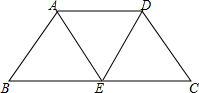 如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是
如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是