题目内容
如图,直角坐标系中直线AB交x轴,y轴于点A(4,0)与B(0,-3),现有一半径为1的动圆的圆心位于原点处,以每秒1个单位的速度向右作平移运动,则经过 秒后动圆与直线AB相切.
【答案】分析:在直角三角形OAB中,OA=4,OB=3,由勾股定理得AB=5,设⊙P经过x秒后与直线AB相切,过P点作AB的垂线,垂足为Q,PQ=1;
(1)当⊙P在直线AB的左边与直线AB相切时,AP=4-x,根据△APQ∽△ABO中的成比例线段求解;
(2)当⊙P在直线AB的右边与直线AB相切时,AP=x-4,根据△APQ∽△ABO中的成比例线段求解.
解答: 解:∵OA=4,OB=3,
解:∵OA=4,OB=3,
∴AB=5,
设⊙P经过x秒后与直线AB相切,过P点作AB的垂线,垂足为Q,则PQ=1;
(1)当⊙P在直线AB的左边与直线AB相切时,AP=4-x,
由△APQ∽△ABO得,
 =
= ,即
,即 =
= ,
,
解得x= ;
;
(2)当⊙P在直线AB的右边与直线AB相切时,AP=x-4;
由△APQ∽△ABO得,
 =
= ,即
,即 =
= ,
,
解得x= .
.
故填 或
或 .
.
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.
(1)当⊙P在直线AB的左边与直线AB相切时,AP=4-x,根据△APQ∽△ABO中的成比例线段求解;
(2)当⊙P在直线AB的右边与直线AB相切时,AP=x-4,根据△APQ∽△ABO中的成比例线段求解.
解答:
 解:∵OA=4,OB=3,
解:∵OA=4,OB=3,∴AB=5,
设⊙P经过x秒后与直线AB相切,过P点作AB的垂线,垂足为Q,则PQ=1;
(1)当⊙P在直线AB的左边与直线AB相切时,AP=4-x,
由△APQ∽△ABO得,
 =
= ,即
,即 =
= ,
,解得x=
 ;
;(2)当⊙P在直线AB的右边与直线AB相切时,AP=x-4;
由△APQ∽△ABO得,
 =
= ,即
,即 =
= ,
,解得x=
 .
.故填
 或
或 .
.点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
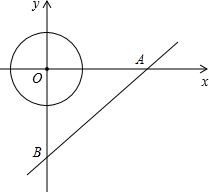 如图,直角坐标系中直线AB交x轴,y轴于点A(4,0)与B(0,-3),现有一半径为1的动圆的圆心位于原点处,以每秒1个单位的速度向右作平移运动,则经过
如图,直角坐标系中直线AB交x轴,y轴于点A(4,0)与B(0,-3),现有一半径为1的动圆的圆心位于原点处,以每秒1个单位的速度向右作平移运动,则经过

