题目内容
4．
如图，在直角坐标系中，设一动点M自P0（1，0）初向上运动1个单位至P1（1，1），然后向左运动2个单位至P2处，再向下运动3个单位至P3处，再向右运动4个单位至P4处，再向上运动5个单位至P5处，…如此继续运动下去，设Pn（xn，yn），n=1，2，3，…则x1+x2+…+x7=-1；以此类推，x1+x2+…+x2014+x2015=-1．
分析 根据各点横坐标数据得出规律，进而得出x1+x2+…+x7；经过观察分析可得每4个数的和为2，把2015个数分为504组，即可得到相应结果．
解答 解：根据平面坐标系结合各点横坐标得出：x1、x2、x3、x4、x5、x6、x7、x8的值分别为：1，-1，-1，3，3，-3，-3，5；
∴x1+x2+…+x7=-1
∵x1+x2+x3+x4=1-1-1+3=2；
x5+x6+x7+x8=3-3-3+5=2；
…
x97+x98+x99+x100=2…
∴x1+x2+…+x2012=2×（2012÷4）=1006．
而x2013、x2014、x2015的值分别为：1007、-1007、-1007，
∴x2013+x2014+x2015=-1007，
∴x1+x2+…+x2014+x2015=1006-1007=-1，
故答案为：-1，-1．
点评 此题主要考查了点的坐标特点，解决本题的关键是分析得到4个数相加的规律．
练习册系列答案
相关题目
的非负整数解是__________________
＝
，若存在这样一点，求出点P的坐标，若不存在，试说明理由． 
某班共有52名同学，在校广播操比赛中排成方队，先把每位同学都进行编号，然后把各自的位置固定下来，如图，在平面直角坐标系中，每个自然数都对应着一个坐标．例如1的对应点是原点（0，0），3的对应点是（1，1），16的对应点是（-1，2）．那么最后一名同学的位置对应的坐标是（4，-1），全校学生如果排成这样一个大方阵，编号是2015的学生的对应点的坐标是（12，-22）．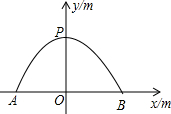
一个横截面为抛物线形的隧道底部宽AB为12m，最大高度OP为6m，如图，车辆双向通行，规定车辆必须在中心线右侧，距道路边缘2m这一范围内行驶，并保持车辆顶部与隧道有不少于0.4m的空隙，现以AB中点O为原点，AB所在直线为x轴建立直角坐标系．
如果将点P绕定点M旋转180°后与点Q重合，那么点P与点Q关于点M对称，定点M叫做对称中心，此时，点M是线段PQ的中点，如图，在直角坐标系中，△ABO的顶点A、B、O的坐标分别为（1，0），（0，1），（0，0），点列P1、P2、P3…中的相邻两点都关于△ABO的一个顶点对称，点P1与点P2关于点A对称，点P2与点P3关于点B对称，点P3与点P4关于点O对称，点P4与点P5关于点A对称，点P5与点P6关于点B对称，点P6与点P7关于点O对称，且这些对称中心依次循环，已知点P1的坐标是（1，1），则点P2015的坐标为（1，3）．
11．下列说法，（1）如果a，b互为倒数，则ab=1；（2）如果a，b互为相反数，则（a+b）=0；（3）几个有理数相乘，如果负因数的个数为奇数个，则积为负；（4）一个非0有理数一定小于它的2倍，其中错误的有（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
12．现有一个正八边形的纸片，则该纸片每个内角的外角的度数为（ ）
| A． | 60° | B． | 50° | C． | 45° | D． | 30° |