题目内容
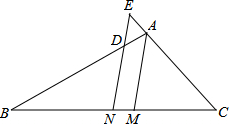如图，AM为△ABC的角平分线，BD=CE，NE∥AM，求证：N为BC中点．考点：平行线分线段成比例
专题：证明题
分析：先根据角平分线定理得到
=
，即
=
，再根据三条平行线截两条直线，所得的对应线段成比例得到
=
，即BN=
，
=
，即CN=
，易得BN=CN．
| AB |
| AC |
| BM |
| CM |
| AB |
| BM |
| AC |
| CM |
| BN |
| BM |
| BD |
| BA |
| BM•BD |
| AB |
| CN |
| CM |
| CE |
| CA |
| CM•CE |
| AC |
解答：证明：∴AM为△ABC的角平分线，
∴
=
，即
=
∵ND∥AM，
∴
=
，即BN=
，
∵AM∥NE，
∴
=
，即CN=
，
∵BD=CE，
∴BN=CN，
即N为BC的中点．
∴
| AB |
| AC |
| BM |
| CM |
| AB |
| BM |
| AC |
| CM |
∵ND∥AM，
∴
| BN |
| BM |
| BD |
| BA |
| BM•BD |
| AB |
∵AM∥NE，
∴
| CN |
| CM |
| CE |
| CA |
| CM•CE |
| AC |
∵BD=CE，
∴BN=CN，
即N为BC的中点．
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例；平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例；如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
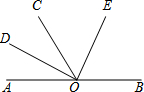如图，点O是直线AB上的一点，∠AOC=60°，OD、OE分别是∠AOC、∠BOC的角平分线．