��Ŀ����
����Ŀ����������֪����ͼ�٣���֪![]() ����
����![]() �ڲ�������
�ڲ�������![]() ���õ������ǣ��ֱ�Ϊ
���õ������ǣ��ֱ�Ϊ![]() ��
��![]() ��
��![]() ����������������һ����������һ���ǵ��������������
����������������һ����������һ���ǵ��������������![]() Ϊ
Ϊ![]() �ġ��������ߡ���
�ġ��������ߡ���
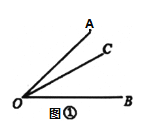
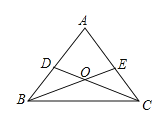
��1��һ���ǵĽ�ƽ����______����ǵġ��������ߡ�����ǡ����ǡ���
��2����![]() ������
������![]() Ϊ
Ϊ![]() �ġ��������ߡ�����
�ġ��������ߡ�����![]() �Ĵ�С��______��
�Ĵ�С��______��
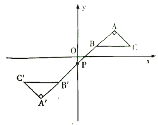
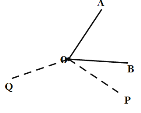
��������⣩��ͼ�ڣ���֪![]() ������
������![]() ��
��![]() ��������
��������![]() /����ٶ���
/����ٶ���![]() ����ʱ����ת������
����ʱ����ת������![]() ��
��![]() ��������
��������![]() /����ٶ���
/����ٶ���![]() ��˳ʱ����ת������
��˳ʱ����ת������![]() ��
��![]() ͬʱ������������һ�����ص�����λ�õ�ʱ�������˶���ֹ֮ͣ�����˶���ʱ��Ϊ
ͬʱ������������һ�����ص�����λ�õ�ʱ�������˶���ֹ֮ͣ�����˶���ʱ��Ϊ![]() �룮
�룮
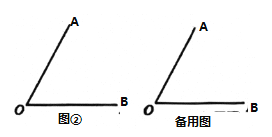
��3��������![]() ��
��![]() ��ת��ͬһ��ֱ����ʱ����
��ת��ͬһ��ֱ����ʱ����![]() ��ֵ��
��ֵ��
��4����![]() ��
��![]() ��
��![]() ���������У�һ������ǡ������������������Ϊ����ɵĽǵġ��������ߡ���ֱ��д��
���������У�һ������ǡ������������������Ϊ����ɵĽǵġ��������ߡ���ֱ��д��![]() ���п��ܵ�ֵ______��
���п��ܵ�ֵ______��
���𰸡���1���ǣ���2��![]() ��
��![]() ��
��![]() ����3��
����3��![]() ��
��![]() ��
��![]() ����4��
����4��![]() ��
��![]() .
.
��������
��1����OCΪ![]() �Ľ�ƽ���ߣ��ɽ�ƽ���ߵĶ���ɵ�
�Ľ�ƽ���ߣ��ɽ�ƽ���ߵĶ���ɵ�![]() ���ɶ������ߵĶ����֪���ۣ�
���ɶ������ߵĶ����֪���ۣ�
��2�����ݶ������ߵĶ����![]() ����������
����������![]() �Ĵ�С����.
�Ĵ�С����.
��3��������![]() ��
��![]() ��ת��ͬһ��ֱ����ʱ��
��ת��ͬһ��ֱ����ʱ��![]() ����
����![]() ��
��![]() ����OP��OQ�غ�ʱ����
����OP��OQ�غ�ʱ����![]() ���ú�t��ʽ�ӱ�ʾ��OP��OQ��ת�ĽǶȴ����������������⼴�ɣ�
���ú�t��ʽ�ӱ�ʾ��OP��OQ��ת�ĽǶȴ����������������⼴�ɣ�
��4����ϡ��������ߡ��Ķ��壬����t��ȡֵ��Χ��![]() ��
��![]() ��
��![]() ��
��![]() 4��������ۼ���.
4��������ۼ���.
�⣺��1����OCΪ![]() �Ľ�ƽ���ߣ��ɽ�ƽ���ߵĶ���ɵ�
�Ľ�ƽ���ߣ��ɽ�ƽ���ߵĶ���ɵ�![]() ���ɶ������ߵĶ����֪һ���ǵĽ�ƽ����������ǵġ��������ߡ���
���ɶ������ߵĶ����֪һ���ǵĽ�ƽ����������ǵġ��������ߡ���
��2��������![]() Ϊ
Ϊ![]() �ġ��������ߡ�ʱ����3�������
�ġ��������ߡ�ʱ����3�������
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
�ۺ�������![]() �Ĵ�СΪ
�Ĵ�СΪ![]() ��
��![]() ��
��![]() ��
��
��3��������![]() ��
��![]() ��ת��ͬһ��ֱ����ʱ��������3�������
��ת��ͬһ��ֱ����ʱ��������3�������
����ͼ
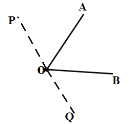
��ʱ![]() ����
����![]() �����
�����![]() ��
��
����ͼ
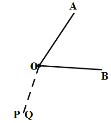
��ʱ��P�͵�Q�غϣ��ɵ�![]() ����
����![]() �����
�����![]() ��
��
����ͼ
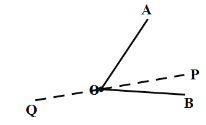
��ʱ![]() ����
����![]() �����
�����![]() ��
��
�ۺ�������![]() ��
��![]() ��
��![]() ��
��
��4���������˶�ֹͣʱ![]() ������
������![]() ��
��
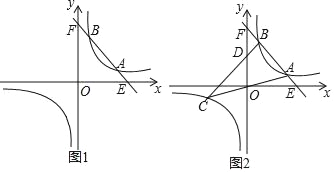
�ٵ�![]() ʱ����ͼ��
ʱ����ͼ��
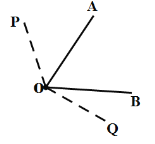
��ʱOAΪ![]() �����������ߡ���
�����������ߡ���![]() ��
��
��![]() �����
�����![]() ��
��
����![]() ʱ����ͼ��
ʱ����ͼ��
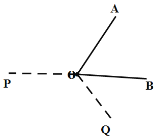
��ʱ��![]() �����Բ����ڣ�
�����Բ����ڣ�
�۵�![]() ʱ����ͼ
ʱ����ͼ
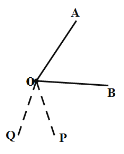
��ʱOPΪ![]() �ġ��������ߡ���
�ġ��������ߡ���![]() ��
��
��![]()
��� ![]() ��
��
����![]() ʱ����ͼ��
ʱ����ͼ��
��ʱ![]() �����Բ����ڣ�
�����Բ����ڣ�
������������![]() ��
��![]() ʱ��
ʱ��![]() ��
��![]() ��
��![]() ���������У�һ������ǡ������������������Ϊ����ɵĽǵġ��������ߡ�.
���������У�һ������ǡ������������������Ϊ����ɵĽǵġ��������ߡ�.

����Ŀ��ij��ѧΪ�˿�ѧ������ѧ�������ɳ��������������ȡ�˲���ѧ����ͥ����ҳ�����������Ϊ����ĩ�����ڼ��������������ʾ����飬�����յ��ʾ����з����������õ������µ�����ͳ�Ʊ�������ͳ��ͼ��
���� | ������� | ��ͥ�� |
| �������沢�ҹ�������ҵ������ | 16 |
| ֻ��������ҵ������ | b |
| ֻ�������� | 8 |
| �Ȳ���������Ҳ����������ҵ������ | d |
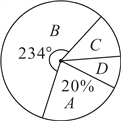
��1����![]() ��ֵ��
��ֵ��
��2����Уѧ����ͥ����Ϊ500��ѧУ������������![]() ���ͥ�г�ȡ�ҳ������ѵ�࣬�����Ϊ
���ͥ�г�ȡ�ҳ������ѵ�࣬�����Ϊ![]() ��ȡ20%��
��ȡ20%��![]() ���ȡ60%��������Ƹ���ѵ��ļ�ͥ����
���ȡ60%��������Ƹ���ѵ��ļ�ͥ����
��3������![]() ���ͥ��ֻ��һ�������ͥ��������ũ���ͥ�������оٷ������
���ͥ��ֻ��һ�������ͥ��������ũ���ͥ�������оٷ������![]() ����������2����ͥ������Ȳɷã�������һ���dz����ͥ�ĸ��ʣ�
����������2����ͥ������Ȳɷã�������һ���dz����ͥ�ĸ��ʣ�