Question

如图，AC为⊙O的直径，AC=4，B、D分别在AC两侧的圆上，∠BAD=60°，BD与AC的交点为E．
(1) 求点O到BD的距离及∠OBD的度数；
(2) 若DE=2BE，求的值和CD的长．

Answer 1

解：（1）作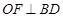于点F，连结OD．（如图4）
∵ ∠BAD=60°，
∴ ∠BOD="2∠BAD" =120°．
又∵OB=OD，
∴ ．
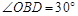∵ AC为⊙O的直径，AC=4，
∴ OB=" OD=" 2．
在Rt△BOF中，∵∠OFB=90°， OB=2，，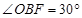
∴ ，
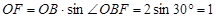即点O到BD的距离等于1.
（2）∵ OB= OD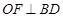，于点F，
∴ BF=DF．
由DE=2BE，设BE=2x，则DE=4x，BD=6x，EF=x，BF=3x．
∵ ，
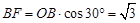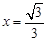∴ ， EF=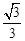．www.xkb1.com
在Rt△OEF中，，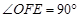

∵，
∴ ，．
∴ ．
∴ ．
∴ ．
∴ ．

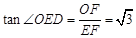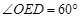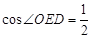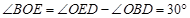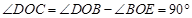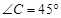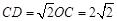解析