题目内容
 已知如图,圆内接四边形ABCD,AB=AD,PB=BO,CE⊥PE,CD=18,求DE.
已知如图,圆内接四边形ABCD,AB=AD,PB=BO,CE⊥PE,CD=18,求DE.
分析:连OA,由AB=AD,得∠AOB=∠DCO,OA∥DC,得到
=
=
=
,则OA=
×18=12,PA=2AD;再根据由切割线定理得,PB•PC=PA•PD,即可得到AD=6
;然后过O作OF⊥AB于F点,可证明Rt△CDE~Rt△OBF,通过相似比求出DE.
| PA |
| PD |
| PO |
| PC |
| OA |
| CD |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答: 解:连OA,如图,
解:连OA,如图,
∵AB=AD,
∴∠AOB=∠DCO,
∴OA∥DC,
而PB=BO,CD=18
∴
=
=
=
,则OA=
×18=12,PA=2AD,
由切割线定理得,PB•PC=PA•PD,即12×36=2AD•3AD,所以AD=6
,
过O作OF⊥AB于F点,则BF=AF=3
,
∵∠EDC=∠ABO,且CE⊥PE,
∴Rt△CDE~Rt△OBF,
∴
=
,即
=
,
∴DE=
.
 解:连OA,如图,
解:连OA,如图,∵AB=AD,
∴∠AOB=∠DCO,
∴OA∥DC,
而PB=BO,CD=18
∴
| PA |
| PD |
| PO |
| PC |
| OA |
| CD |
| 2 |
| 3 |
| 2 |
| 3 |
由切割线定理得,PB•PC=PA•PD,即12×36=2AD•3AD,所以AD=6
| 2 |
过O作OF⊥AB于F点,则BF=AF=3
| 2 |
∵∠EDC=∠ABO,且CE⊥PE,
∴Rt△CDE~Rt△OBF,
∴
| DE |
| BF |
| CD |
| OB |
| DE | ||
3
|
| 18 |
| 12 |
∴DE=
9
| ||
| 2 |
点评:本题考查了圆周角定理.在同圆或等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查了平行线分线段成比例定理、切割线定理、圆内接四边形的性质和三角形相似的判定与性质.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
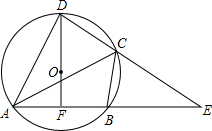 已知:如图,圆内接四边形ABCD的两边AB、DC的延长线相交于点E,DF过圆心O交AB于点F,AB=BE,连接AC,且OD=3,AF=FB=
已知:如图,圆内接四边形ABCD的两边AB、DC的延长线相交于点E,DF过圆心O交AB于点F,AB=BE,连接AC,且OD=3,AF=FB= 如图,圆内接四边形ABCD的两条对角线交于点P.已知AB=BC,CD=
如图,圆内接四边形ABCD的两条对角线交于点P.已知AB=BC,CD= 已知如图,圆内接四边形ABCD,AB=AD,PB=BO,CE⊥PE,CD=18,求DE.
已知如图,圆内接四边形ABCD,AB=AD,PB=BO,CE⊥PE,CD=18,求DE.