Question

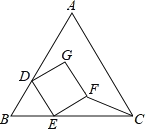
【题目】如图，在△ABC中，AB=8，AC=6．点D在边AB上，AD=4.5．△ABC的角平分线AE交CD于点F．

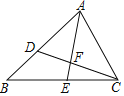
（1）求证：△ACD∽△ABC；

（2）求的值．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

（1）由AB，AC，AD的长可得出，结合∠CAD=∠BAC即可证出△ACD∽△ABC；

（2）利用相似三角形的性质可得出∠ACD=∠B，由AE平分∠BAC可得出∠CAF=BAE，进而可得出△ACF∽△BAE，再利用相似三角形的性质即可求出的值．

（1）证明：∵AB=8，AC=6，AD=4.5，

∴．

又∵∠CAD=∠BAC，

∴△ACD∽△ABC；

（2）∵△ACD∽△ABC，

∴∠ACD=∠B．

∵AE平分∠BAC，

∴∠CAF=BAE，

∴△ACF∽△BAE，

∴．