题目内容
如图,在△ABC中,AE是∠BAC的角平分线,AD是BC边上的高,且∠B = 40º, ∠C = 60º,求∠CAD、∠EAD的度数。(6分)

【解析】
∵AD是BC边上的高,∠C=60°,
∴∠CAD=90°-∠C=90°-60°=30°;
在△ABC中,∠BAC=180°-∠B-∠C=180°-40°-60°=80°,
∵AE是∠BAC的角平分线,
∴∠CAE= ∠BAC=
∠BAC= ×80°=40°,
×80°=40°,
∴∠EAD=∠CAE-∠CAD=40°-30°=10°.
【解析】
试题分析:根据直角三角形两锐角互余可得∠CAD=90°-∠C,再利用三角形的内角和定理求出∠BAC,根据角平分线的定义求出∠CAE,然后根据∠EAD=∠CAE-∠CAD计算即可得解.∴∠EAD=∠CAE-∠CAD=40°-30°=10°.
考点:三角形的内角和定理

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 的图象如下图所示,则结论:
的图象如下图所示,则结论:
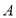 的坐标为
的坐标为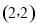 ;
; 时,
时, ;
; 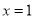 时,
时,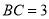 ;
;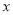 逐渐增大时,
逐渐增大时,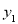 随着
随着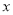 的增大而增大,
的增大而增大,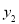 随着
随着 B.
B. C.
C. D.
D.
