Question

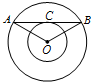
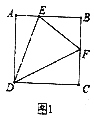
【题目】（1）如图①，四边形为正方形，点分别在与上，且，求证：．

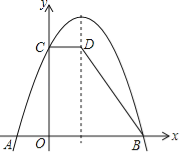
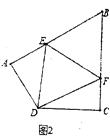
（2）如图②，在四边形中，，点分别在与上，且.猜想与之间的数量关系，并证明你的猜想；

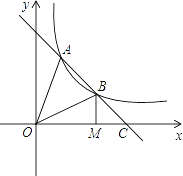
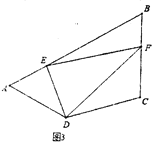
（3）如图③，在四边形中，与互补，点分别在与上，且，请直接写出，与之间的数量关系．

Answer 1

【答案】（1）见解析；（2），详见解析；（3），详见解析

【解析】

（1）延长至点G，使AG=CF，根据正方形的性质证明△ADG≌△CDF，得到∠ADG=∠CDF，DG=DF，再证明△DEG≌△DEF，即可得到结论；

（2）延长BC至点H，使CH=AE，连接DH，同（1）的方法证明即可得到结论；

（3），延长BC至点M，使CM=AE，连接DM，同上的证明方法即可得到结论.

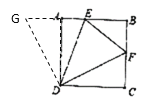
（1）如图，延长至点G，使AG=CF，连接DG，

∵四边形为正方形，

∴AD=CD，∠BAD=∠ADC=∠C=90°，

∴△ADG≌△CDF，

∴∠ADG=∠CDF，DG=DF，

∵,

∴∠ADG+∠CDF=∠ADE+∠CDF=45°，

∵DE=DE，

∴△DEG≌△DEF，

∴EF=GE=AG+AE=CF+AE，

∴；

（2）AE+CF=EF，

延长BC至点H，使CH=AE，连接DH，

∵∠A=∠BCD=90°，

∴∠A=∠DCH=90°，

∵AD=CD，AE=CH，

∴△ADE≌△CDH，

∴DE=DH，∠ADE=∠CDH，

∵∠ADC=120°，

∴∠EDH=120°，

∵∠EDF=60°，

∴∠HDF=∠EDF=60°，

又∵CD=CD，

∴△EDF≌△HDF，

∴EF=HF=CF+CH=AE+CF；

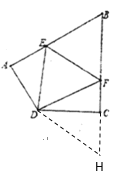
（3），

延长BC至点M，使CM=AE，连接DM，

∵∠DAB与∠BCD互补，

∴∠DAB+∠BCD==180°，

∴∠DAB=∠DCM，

∵AD=CD，AE=CM，

∴△ADE≌△CDM，

∴DE=DM，∠ADE=∠CDM，

∵,,

∴∠MDF=,

又∵DF=DF，

∴△EDF≌△MDF，

∴EF=MF=CM+CF=AE+CF.