Question

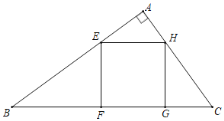
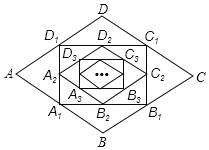
【题目】问题：如图1，等腰直角三角形中，，点、点分别在边上，且，显然．

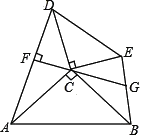
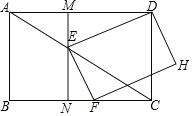
变式：若将图1中的绕点逆时针旋转，使得点在的内部，其它条件不变（如图2），请你猜想线段与线段的关系，并加以证明．

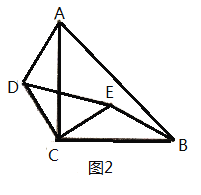
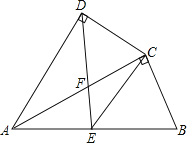
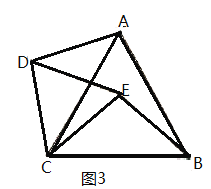
拓展：若图2中的、都为等边三角形，其它条件不变（如图3），则__________，直线与相交所夹的锐角为__________°．

Answer 1

【答案】变式：，证明详见解析；拓展：，．

【解析】

变式:观察图形,根据已知条件,考虑等腰直角三角形的性质和旋转的性质,推断出,即可得到的数量关系,延长交于点,根据角度等量代换,即可得到的位置关系.

拓展: 观察图形,根据已知条件,考虑等边三角形的性质和旋转的性质,推断出,即可得到的数量关系,延长交于点,根据角度等量代换,即可得到的位置关系

变式：答：

证明：如图,

延长交于点，

∴

∴，

∴,

∴．

拓展：如图,延长交于点,

∴

∴,

∴,

∴.