题目内容
在⊙O中,AB是直径,CD是弦(非直径),AB⊥CD,现有直线k经过点D旋转交⊙O于P,当直线k经过点A时(如图1)易证:∠DPB+∠C=90°.(1)当点P在
 上时(如图2),“∠DPB+∠C=90°”还成立吗?试证明你的结论;
上时(如图2),“∠DPB+∠C=90°”还成立吗?试证明你的结论;(2)在直线k绕点D旋转的过程中(不考虑P与B或D重合的情形),∠DPB与∠C有几种不同的数量关系?写出与“∠DPB+∠C=90°”不同的关系式(仍用等式表示),并说明点P相应的位置和理由.

【答案】分析:(1)利用圆周角定理可得∠DPB=∠A;然后根据垂径定理、直角三角形的两个锐角互余的性质证得该结论成立;
(2)有两种不同的数量关系:“∠DPB+∠C=90°”和“∠DPB-∠C=90°”.连接AP,BP.由圆周角定理(直径所对的圆周角是直角)推知∠BPA=90°,由等弧所对的圆周角相等证得∠C=∠APD;然后根据图形中的相关角间的数量关系知∠BPD=∠BPA+∠APD,即∠BPD-∠C=90°.
解答: (1)如图1所示:点在
(1)如图1所示:点在 上时,∠DPB+∠C=90°,仍成立.
上时,∠DPB+∠C=90°,仍成立.
证明:∵AB⊥CD,∴CE=DE,
∴ =
= ,
,
∵∠DPB=∠A(等弧所对的圆周角相等);
又∵∠A+∠C=90°,
∴∠DPB+∠C=90°(等量代换);
(2)有两种不同的数量关系:“∠DPB+∠C=90°(如图1所示)”和“∠DPB-∠C=90°(如图2所示)”.
当点P在 上时,∠DPB-∠C=90°;
上时,∠DPB-∠C=90°;
证明:连接AP,BP.∠BPD=∠BPA+∠APD,
∵AB是直径,
∴∠BPA=90°;
∵∠C=∠APD,
∴∠BPD=90°+∠C,即:∠BPD-∠C=90°.
点评:本题考查了圆的综合题:在同圆或等圆中,相等的弧所对的圆周角相等,直径所对的圆周角为直角;垂直于弦的直径平分弦,并且平分弦所对的弧.
(2)有两种不同的数量关系:“∠DPB+∠C=90°”和“∠DPB-∠C=90°”.连接AP,BP.由圆周角定理(直径所对的圆周角是直角)推知∠BPA=90°,由等弧所对的圆周角相等证得∠C=∠APD;然后根据图形中的相关角间的数量关系知∠BPD=∠BPA+∠APD,即∠BPD-∠C=90°.
解答:
 (1)如图1所示:点在
(1)如图1所示:点在 上时,∠DPB+∠C=90°,仍成立.
上时,∠DPB+∠C=90°,仍成立.证明:∵AB⊥CD,∴CE=DE,
∴
 =
= ,
,∵∠DPB=∠A(等弧所对的圆周角相等);
又∵∠A+∠C=90°,
∴∠DPB+∠C=90°(等量代换);
(2)有两种不同的数量关系:“∠DPB+∠C=90°(如图1所示)”和“∠DPB-∠C=90°(如图2所示)”.
当点P在
 上时,∠DPB-∠C=90°;
上时,∠DPB-∠C=90°;
证明:连接AP,BP.∠BPD=∠BPA+∠APD,
∵AB是直径,
∴∠BPA=90°;
∵∠C=∠APD,
∴∠BPD=90°+∠C,即:∠BPD-∠C=90°.
点评:本题考查了圆的综合题:在同圆或等圆中,相等的弧所对的圆周角相等,直径所对的圆周角为直角;垂直于弦的直径平分弦,并且平分弦所对的弧.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 4、如图,在⊙O中,AB是⊙O直径,∠BAC=40°,则∠ADC的度数是( )
4、如图,在⊙O中,AB是⊙O直径,∠BAC=40°,则∠ADC的度数是( ) (2013•海沧区一模)已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.
(2013•海沧区一模)已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D. (2012•邢台二模)如图,在⊙O中,AB是直径,∠OCA=26°,则∠BOC=( )
(2012•邢台二模)如图,在⊙O中,AB是直径,∠OCA=26°,则∠BOC=( )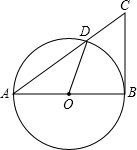 (2012•延庆县二模)已知:在⊙O中,AB是直径,CB是⊙O的切线,连接AC与⊙O交于点D,
(2012•延庆县二模)已知:在⊙O中,AB是直径,CB是⊙O的切线,连接AC与⊙O交于点D, (2012•宜宾)如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是
(2012•宜宾)如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是