题目内容
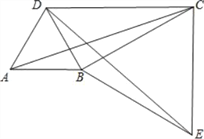
【题目】如图1，在平面直角坐标系中，点A（a，0），B（b，3），C（c，0），满足
+
+
=0．
（1）分别求出点
，
，
的坐标及三角形ABC的面积．
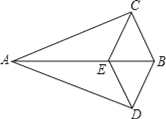
（2）如图2．过点C作
于点D，F是线段AC上一点，满足
，若点G是第二象限内的一点，连接DG，使
，点E是线段AD上一动点（不与A、D重合），连接CE交DF于点H，点E在线段AD上运动的过程中，
的值是否会变化？若不变，请求出它的值；若变化，请说明理由．
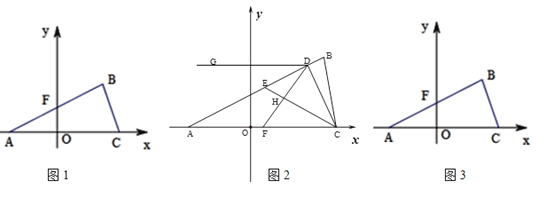
（3）如图3，若线段AB与
轴相交于点F，且点F的坐标为（0，
），在坐标轴上是否存在一点P，使三角形ABP和三角形ABC的面积相等？若存在，求出P点坐标．若不存在，请说明理由．（点C除外）
【答案】（1）
，
，
，
；（2）不变，
；（3）存在一点P，使三角形ABP和三角形ABC的面积相等，点
或
或
．
【解析】
（1）根据非负数的性质可得出a,b,c的值，进而得出点
，
，
的坐标及三角形ABC的面积；
（2）根据已知条件，表达出∠CED、∠DHC，进而求出待求代数式的值；
（3）点P在x轴或在y轴上进行分类讨论，对三角形ABP的面积进行分割，从而求出点P的坐标．
解：（1）∵
+
+
=0，
∴
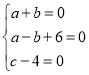，解得：
，
∴，，
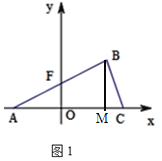
如图，过点B作
，
则AC=7，BM=3，
∴
，
（2）不变，
∵
，
∴∠ADC=90°，
∴∠DAC+∠FCD=90°，
∠FDC+∠ADF=90°，
∵
∴∠DAC=∠ADF，
∴∠CED=∠ACE+∠DAC
∠DHC=∠CED+∠ADF=∠ACE+∠DAC+∠DAC=∠ACE+2∠DAC
∴
，
∴
的值不变，；
（3）存在，
①当点P在x轴上时，则AF=AC=7，因为点P不与点C重合，所以点；
②当点P在y轴上时，设P（0,t）
则PF=
,
∴
=4
∴
，
解得
或
，
所以或
综上，存在一点P，使三角形ABP和三角形ABC的面积相等，点或
或
．
