题目内容
如图，∠A=55°，∠ABD=25°，∠ACO=40°，那么∠BDC=________，∠BOC=________．
80° 120°
分析：根据三角形外角定理可知∠BDC=∠A+∠ABD，∠BOC=∠AC0+∠BDC．
解答：∵∠A=55°，∠ABD=25°（已知），
∴∠BDC=∠A+∠ABD=80°（外角定理）；
又∵∠ACO=40°（已知），
∴∠BOC=∠BDC+∠ACO=120°（外角定理）．
故答案是：80°、120°．
点评：本题考查了三角形的外角性质．三角形的外角通常情况下是转化为内角来解决．
分析：根据三角形外角定理可知∠BDC=∠A+∠ABD，∠BOC=∠AC0+∠BDC．
解答：∵∠A=55°，∠ABD=25°（已知），
∴∠BDC=∠A+∠ABD=80°（外角定理）；
又∵∠ACO=40°（已知），
∴∠BOC=∠BDC+∠ACO=120°（外角定理）．
故答案是：80°、120°．
点评：本题考查了三角形的外角性质．三角形的外角通常情况下是转化为内角来解决．
练习册系列答案
阅读快车系列答案
相关题目
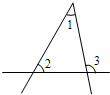（2012•开平区二模）如图，∠1=55°，∠3=108°，则∠2的度数为（ ）
如图，∠B=55°，∠EAC=110°，AD平分∠EAC，AD与BC平行吗？为什么？根据下面的解答过程，在括号内填空或填写理由．
已知：如图，∠1=55°，∠2=35°，点O在直线a上，且OA⊥OB，则a与b的位置关系是
如图，∠A=55°，∠ABD=25°，∠ACO=40°，那么∠BDC=
如图，如果∠