Question

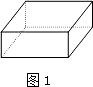
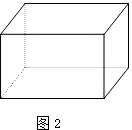
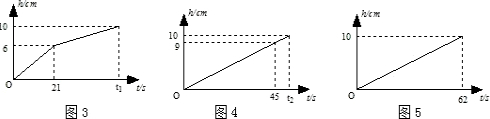
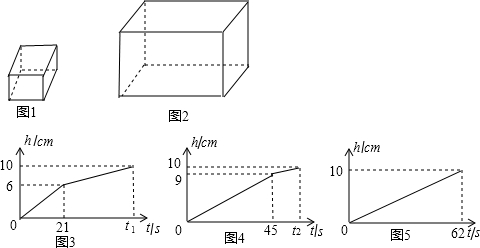
将一块 a （cm）×b （cm ）×c （cm） （a＜b＜c）的长方体铁块（如图1所示）放入一长方体水槽（如图2所示）内，铁块与水槽四壁不接触．现向水槽内匀速注水，直至注满水槽为止．因为铁块在水槽内有三种不同的放置方式，所以水槽内的水深h （cm）与注水时间 t （s）的函数关系用图象法来反映其全过程有三个不同的图象，如图3、4、5所示（说明：三次注水速度相同）．

（1）根据图象填空
①水槽的深度是

10

cm，a=

6cm

，b=

9cm

；
②t₁与t₂的大小关系是t₁

=

t₂，并求出t₁、t₂的值；
（2）求水槽内的底面积和注水速度；
（3）求c的值．

Answer 1

分析：（1）①由图3、4水深到10cm以后不在增加，可知水槽深10cm，由图3可知长方体的最短棱长a的值，由图4可知处于中间的棱长b的值；
②根据水槽的容积等于长方体的体积与注入水的体积，又注入水的速度相同，所以时间t₁与t₂相等；设水槽的底面积为s，根据图3图4刚好没过长方体时的注入水量表示出注入水的速度相同列式整理得到s与c的关系，然后用c表示出注入速度，再根据图3，求出注入剩下的4cm所用的时间，加上21即可得到t₁的值，也就是t₂的值；
（2）根据图5注入水的体积等于水槽中水的高度×（水槽的底面积-a、b为底面的面积），计算即可求出c的值，然后再代入水槽底面积表达式与速度表达式计算即可得解；
（3）在（2）中已求．

解答：解：（1）①由图3、图4可知水槽深度是10cm，
由图3知a=6cm，由图4可知b=9cm，
②前两种是完全浸没的，注水容积相同，
所以t₁=t₂，
设水槽底面积为s，
根据图3、4，注入水的速度为

6(s-9c)

21

=

9(s-6c)

45

，
整理得，10s-90c=7s-42c，
解得s=16c，
所以，注水速度为，

6(s-9c)

21

=

6(16c-9c)

21

=2c，
由图3，

(10-6)s

2c

=

4×16c

2c

=32秒，
∴t₁=21+32=53秒；
t₂=t₁=53秒；
故答案为：①10，6cm，9cm，②=；

（2）根据图5，注入水的体积=10（s-6×9）=62×2c，
即10（16c-54）=124c，
解得c=15，
所以，水槽的底面积为s=16c=16×15=240cm²，
注水速度为2c=2×15=30cm³/s；

（3）c=15cm（上一问已求）．

点评：本题考查了一次函数的应用，仔细观察图形，明确注入水的体积与水槽的容积以及长方体的体积之间的关系，然后根据注入水的速度，利用图3、图4列出方程求出水槽的底面积与c的关系式是解题的关键．