题目内容
 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3在x轴上.若正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是
| ||
| 6 |
| ||
| 6 |
分析:根据两直线平行,同位角相等可得∠B3C3O=∠B2C2O=∠B1C1O=60°,然后解直角三角形求出OC1、C1E、E1E2、E2C2、C2E3、E3E4、E4C3,再求出B3C3,过点A3延长正方形的边交x轴于M,过点A3作A3N⊥x轴于N,先求出A3M,再解直角三角形求出A3N,得出点A3到x轴的距离.
解答: 解:如图,∵B1C1∥B2C2∥B3C3,
解:如图,∵B1C1∥B2C2∥B3C3,
∴∠B3C3O=∠B2C2O=∠B1C1O=60°,
∵正方形A1B1C1D1的边长为1,
∴OC1=
×1=
,
C1E=
×1=
,
E1E2=
×1=
,
E2C2=
×
=
,
C2E3=E2B2=
,
E3E4=
×
=
,
E4C3=
×
=
,
∴B3C3=2E4C3=2×
=
,
过点A3延长正方形的边交x轴于M,过点A3作A3N⊥x轴于N,
则A3M=
+
×
=
,
A3N=
×
=
,
∴点A3到x轴的距离是:
.
故答案为:
.
 解:如图,∵B1C1∥B2C2∥B3C3,
解:如图,∵B1C1∥B2C2∥B3C3,∴∠B3C3O=∠B2C2O=∠B1C1O=60°,
∵正方形A1B1C1D1的边长为1,
∴OC1=
| 1 |
| 2 |
| 1 |
| 2 |
C1E=
| ||
| 2 |
| ||
| 2 |
E1E2=
| 1 |
| 2 |
| 1 |
| 2 |
E2C2=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
C2E3=E2B2=
| 1 |
| 2 |
E3E4=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
E4C3=
| ||
| 6 |
| ||
| 3 |
| 1 |
| 6 |
∴B3C3=2E4C3=2×
| 1 |
| 6 |
| 1 |
| 3 |
过点A3延长正方形的边交x轴于M,过点A3作A3N⊥x轴于N,
则A3M=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
3+
| ||
| 9 |
A3N=
3+
| ||
| 9 |
| ||
| 2 |
1+
| ||
| 6 |
∴点A3到x轴的距离是:
| ||
| 6 |
故答案为:
| ||
| 6 |
点评:此题主要考查了正方形的性质以及解直角三角形的知识,得出正方形各边长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
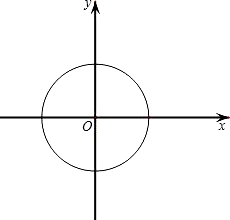 已知在平面直角坐标系xOy中,⊙O的半径为1.
已知在平面直角坐标系xOy中,⊙O的半径为1.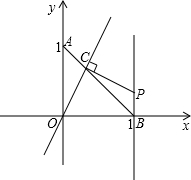 直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y),
直线交线段AB于点C,过点C作OC的垂线与直线x=1相交于点P,设AC=t,点P的坐标为(1,y), 如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.
如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax-2a-1将平行四边形ABCD分成面积相等的两部分,求a的值.