题目内容
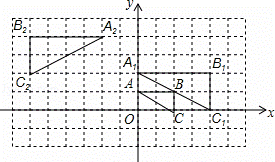
如图,在Rt△AOB中,∠AOB=90°,AO= ,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F.点P从点A出发沿射线AO以每秒2
,BO=1,AB的垂直平分线交AB于点E,交射线BO于点F.点P从点A出发沿射线AO以每秒2 个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动.设运动的时间为t秒.
个单位的速度运动,同时点Q从点O出发沿OB方向以每秒1个单位的速度运动,当点Q到达点B时,点P、Q同时停止运动.设运动的时间为t秒.
(1)当t= 时,PQ∥EF;
(2)若P、Q关于点O的对称点分别为P′、Q′,当线段P′Q′与线段EF有公共点时,t的取值范围是 .

 :0<t≤1且t≠
:0<t≤1且t≠ . 解:(1)如图1,当PQ∥EF时,
. 解:(1)如图1,当PQ∥EF时,
则∠QPO=∠ENA,
又∵∠AEN=∠QOP=90°,
∴△AEN∽△QOP,
∵∠AOB=90°,AO= ,BO=1,
,BO=1,
∴tanA= =
= =
= ,
,
∴∠A=∠PQO=30°,
∴ =
= =
= ,
,
解得:t= ,
,
故当t= 时,PQ∥EF;
时,PQ∥EF;
(2)如图2,∵∠BAO =30°,∠BOA=90°,
=30°,∠BOA=90°,
∴∠B=60°,
∵AB的垂直平分线交AB于点E,
∴FB=FA,
∴△FBA是等边三角形,
∴当PO=OA= 时,此时Q′与F重合,A与P′重合,
时,此时Q′与F重合,A与P′重合,
∴PA=2 ,则t=1秒时,线段P′Q′与线段EF有公共点,
,则t=1秒时,线段P′Q′与线段EF有公共点,
故当t的取值范围是:0<t≤1,由(1)得,t≠ .
.



练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 (k≠0)的图象的一个交点.
(k≠0)的图象的一个交点. 正半轴上的一个动点,设OP=a(a≠2),过点P作垂直于x轴的直线,分别交一次函数,反比例函数的图象于点A,B,过OP的中点Q作x轴的垂线,交反比例函数的图象于点C,△ABC′与△ABC关于直线AB对称.
正半轴上的一个动点,设OP=a(a≠2),过点P作垂直于x轴的直线,分别交一次函数,反比例函数的图象于点A,B,过OP的中点Q作x轴的垂线,交反比例函数的图象于点C,△ABC′与△ABC关于直线AB对称.