题目内容
 如图,已知四边形AOBE和四边形CBFD均为正方形,反比例函数
如图,已知四边形AOBE和四边形CBFD均为正方形,反比例函数 的图象经过D、E两点,则点E的坐标是________;点D的坐标是________;△DOE的面积为________.
的图象经过D、E两点,则点E的坐标是________;点D的坐标是________;△DOE的面积为________.
(2,2) ( -1,
-1, +1) 2
+1) 2
分析:(1)根据正方形的性质,点E的坐标横坐标与纵坐标的相同,所以设出点E的坐标为(a,a),代入函数解析式即可求出;设出正方形CBFD的边长为b,即可用点E的坐标和b表示出点D的坐标代入函数解析式即可求出b的值,点D的坐标即可求出.
(2)根据点D的坐标求出直线OD的解析式,再求出直线与边BE的交点的横坐标,就把△DOE分成了两个三角形,底边已经求出高分别是点E、D的纵坐标的长度,代入三角形的面积公式即可求出.
解答:∵四边形AOBE,∴AO=AE,
设AO=a,则点E为(a,a)
∴ =a,整理得a2=4,
=a,整理得a2=4,
解得a=2,a=-2(舍去),
所以点E的坐标是(2,2),
设正方形CBFD的边长为b,则BF=b,CO=2+b,
所以点D为(b,2+b),
∴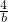 =2+b,整理得b2+2b-4=0,
=2+b,整理得b2+2b-4=0,
解得b= -1,b=-
-1,b=- -1(舍去),
-1(舍去),
所以点D的坐标是( -1,
-1, +1);
+1);
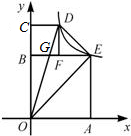
设直线OD与BE的交点为G,则点G的纵坐标为2,
直线OD的解析式为y= x,即y=
x,即y= x,
x,
∴ x=2,
x=2,
解得x=3- ,
,
∴EG=2-(3- )=
)= -1,
-1,
所以S△DOE=S△OEG+S△DEG= ×EG×OB+
×EG×OB+ ×EG×BC
×EG×BC
= ×(
×( -1)×2+
-1)×2+ ×(
×( -1)×(
-1)×( -1)
-1)
=2.
点评:本题主要利用正方形四条边都相等的性质和反比例函数图象的性质求解,图象经过点,则点的坐标满足函数解析式.求面积时,求出直线OD与边BE的交点的横坐标,再把三角形分成两个三角形的面积分别求出是解题的难点,突破了这一点本题也就解决了.
 -1,
-1, +1) 2
+1) 2分析:(1)根据正方形的性质,点E的坐标横坐标与纵坐标的相同,所以设出点E的坐标为(a,a),代入函数解析式即可求出;设出正方形CBFD的边长为b,即可用点E的坐标和b表示出点D的坐标代入函数解析式即可求出b的值,点D的坐标即可求出.
(2)根据点D的坐标求出直线OD的解析式,再求出直线与边BE的交点的横坐标,就把△DOE分成了两个三角形,底边已经求出高分别是点E、D的纵坐标的长度,代入三角形的面积公式即可求出.
解答:∵四边形AOBE,∴AO=AE,
设AO=a,则点E为(a,a)
∴
 =a,整理得a2=4,
=a,整理得a2=4,解得a=2,a=-2(舍去),
所以点E的坐标是(2,2),
设正方形CBFD的边长为b,则BF=b,CO=2+b,
所以点D为(b,2+b),
∴
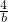 =2+b,整理得b2+2b-4=0,
=2+b,整理得b2+2b-4=0,解得b=
 -1,b=-
-1,b=- -1(舍去),
-1(舍去),所以点D的坐标是(
 -1,
-1, +1);
+1);
设直线OD与BE的交点为G,则点G的纵坐标为2,
直线OD的解析式为y=
 x,即y=
x,即y= x,
x,∴
 x=2,
x=2,解得x=3-
 ,
,∴EG=2-(3-
 )=
)= -1,
-1,所以S△DOE=S△OEG+S△DEG=
 ×EG×OB+
×EG×OB+ ×EG×BC
×EG×BC=
 ×(
×( -1)×2+
-1)×2+ ×(
×( -1)×(
-1)×( -1)
-1)=2.
点评:本题主要利用正方形四条边都相等的性质和反比例函数图象的性质求解,图象经过点,则点的坐标满足函数解析式.求面积时,求出直线OD与边BE的交点的横坐标,再把三角形分成两个三角形的面积分别求出是解题的难点,突破了这一点本题也就解决了.

练习册系列答案
相关题目
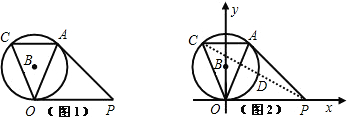
 (2010•北海)如图,已知⊙O上A、B、C三点,∠BAC=30°,D是OB延长线上的点,∠BDC=30°,⊙O半径为
(2010•北海)如图,已知⊙O上A、B、C三点,∠BAC=30°,D是OB延长线上的点,∠BDC=30°,⊙O半径为 如图,已知四边形ABCD中,AD∥BC,AC与BD交于点O,AO=CO,过项点A的直线交BD于点P,交CD于点Q,并交BC的延长线于点R.
如图,已知四边形ABCD中,AD∥BC,AC与BD交于点O,AO=CO,过项点A的直线交BD于点P,交CD于点Q,并交BC的延长线于点R.
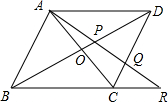 如图,已知四边形ABCD中,AD∥BC,AC与BD交于点O,AO=CO,过项点A的直线交BD于点P,交CD于点Q,并交BC的延长线于点R.
如图,已知四边形ABCD中,AD∥BC,AC与BD交于点O,AO=CO,过项点A的直线交BD于点P,交CD于点Q,并交BC的延长线于点R.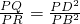 成立吗,若成立,请说明理由.
成立吗,若成立,请说明理由.