题目内容
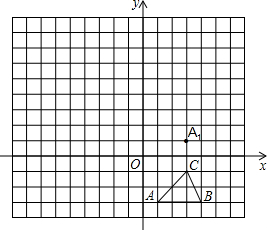
如果△ABC中，∠C=90°，AC=5，BC=12，那么AB边上的中线长是 ．
【答案】分析：根据勾股定理求出AB，根据直角三角形斜边上中线性质求出CD即可．
解答：解：
由勾股定理得：AB=
=
=13，
∵CD是直角三角形ACB斜边AB上的中线，
∴CD=
AB=6.5，
故答案为：6.5．
点评：本题考查了勾股定理和直角三角形斜边上中线性质，注意：直角三角形斜边上的中线等于斜边的一半．
解答：解：
由勾股定理得：AB=
==13，∵CD是直角三角形ACB斜边AB上的中线，
∴CD=
AB=6.5，故答案为：6.5．
点评：本题考查了勾股定理和直角三角形斜边上中线性质，注意：直角三角形斜边上的中线等于斜边的一半．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
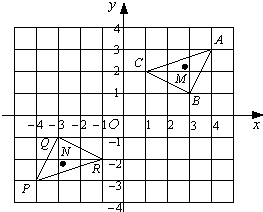15、如图，△PQR是△ABC经过某种变换后得到的图形．如果△ABC中任意一点M的坐标为（a，b），那么它的对应点N的坐标为如果△ABC中，∠A：∠B：∠C=1：2：3，那么BC：AC：AB的值是（ ）
| A、1：2：3 | ||
| B、3：2：1 | ||
C、1：
| ||
D、1：2：
|
