题目内容
如图1—133所示,某船向正东方向航行,在A处望见灯塔C在东北方向,前进到B处,望见灯塔C在北偏 西30°方向,又航行了半小时到达D处,望见灯塔C恰好在西北方向,若船速为每小时20海里,求A,D两点间的距离.(结果不取近似值)
西30°方向,又航行了半小时到达D处,望见灯塔C恰好在西北方向,若船速为每小时20海里,求A,D两点间的距离.(结果不取近似值)

解:过C作CE⊥AD于E,在ΔCED中, ∠CDE=45°.∴CE=DE.在RtΔCEB中,∠CBE=60°,∴BE=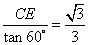 CE ∵BD=DE-BE=20×
CE ∵BD=DE-BE=20× =10 (米),∴CE-
=10 (米),∴CE-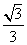 CE=10,∴CE=5(3+
CE=10,∴CE=5(3+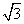 )米.∵∠CAD=∠CDA=45°.∴∠ACD=90°.又∵CE⊥AD,∴AD=2CE=10(3+
)米.∵∠CAD=∠CDA=45°.∴∠ACD=90°.又∵CE⊥AD,∴AD=2CE=10(3+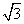 )=(30+10
)=(30+10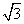 )(海里).答:A,D两点间的距离为(30+10
)(海里).答:A,D两点间的距离为(30+10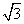 )海里.
)海里.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
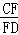 =
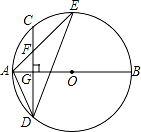
=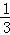 ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3. D;
D;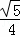 .
.
 c= .
c= . 440 430 450 470 440
440 430 450 470 440