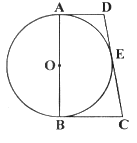
题目内容
如图①,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() 与⊙
与⊙![]() 相切于点
相切于点![]() ,
,![]() 与⊙
与⊙![]() 相切于点
相切于点![]() ,点
,点![]() 为
为![]() 延长线上一点,且CE=CB.
延长线上一点,且CE=CB.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
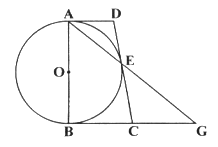
(2)如图②,连接AE,AE的延长线与BC的延长线交于点G .若![]() ,
,
求线段BC和EG的长.
解:(1)连接OE,OC
∵CB=CE,OB=OE,OC=OC
∴△OBC≌△OEC
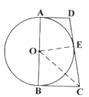 ∴∠OBC=∠OEC………………1分
∴∠OBC=∠OEC………………1分
又∵与DE⊙O相切于点![]()
∴∠OEC=90。
∴∠OBC=90。
∴BC为⊙![]() 的切线
的切线
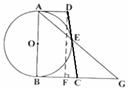 (2)过点D作DF⊥BC于点F,
(2)过点D作DF⊥BC于点F,
∵AD,DC,BG分别切⊙O于点A,E,B
∴DA=DE,CE=CB
设BC为![]() ,则CF=x-2,DC=x+2
,则CF=x-2,DC=x+2
在Rt△DFC中,![]()
解得:![]()
∵AD∥BG∴∠DAE=∠EGC
∵DA=DE∴∠DAE=∠AED
∵∠AED=∠CEG ∴∠ECG=∠CEG
∴CG=CE=CB=![]()
∴BG=5
∴![]()
∵∠DAE=∠EGC ,∠AED=∠CEG
∴△ADE∽△GCE
∴![]() ,
,![]() ,解得
,解得![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 25、如图:AB为⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠DCB=∠A.
25、如图:AB为⊙O的直径,C是⊙O上一点,D在AB的延长线上,且∠DCB=∠A.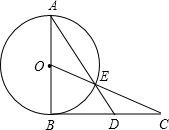 如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.
如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D. 5、如图,AB为⊙O的直径,点C在⊙O上.若∠C=16°,则∠BOC的度数是( )
5、如图,AB为⊙O的直径,点C在⊙O上.若∠C=16°,则∠BOC的度数是( ) (2012•安溪县质检)如图,AB为⊙O的直径,CD为弦,且CD⊥AB于点E,下列结论:①CE=ED;②OE=EB;③AC=AD;④AC=CD.其中正确结论的序号是
(2012•安溪县质检)如图,AB为⊙O的直径,CD为弦,且CD⊥AB于点E,下列结论:①CE=ED;②OE=EB;③AC=AD;④AC=CD.其中正确结论的序号是 如图,AB为半圆的直径,C是半圆弧上一点,正方形DEFG的一边DG在直径AB上,另一边DE过△ABC的内切圆圆心O,且点E在半圆弧上.①若正方形的顶点F也在半圆弧上,则半圆的半径与正方形边长的比是
如图,AB为半圆的直径,C是半圆弧上一点,正方形DEFG的一边DG在直径AB上,另一边DE过△ABC的内切圆圆心O,且点E在半圆弧上.①若正方形的顶点F也在半圆弧上,则半圆的半径与正方形边长的比是