题目内容
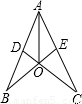
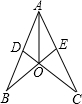 小刚设计了一个玩具模型,如图所示,其中AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD、BE相交于点O,为了使图形美观,小刚希望AO恰好平分∠BAC,他的这个愿望能实现吗?请你帮他说明理由.
小刚设计了一个玩具模型,如图所示,其中AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD、BE相交于点O,为了使图形美观,小刚希望AO恰好平分∠BAC,他的这个愿望能实现吗?请你帮他说明理由.
分析:先根据角角边判定△ABE和△ACD全等,根据全等三角形对应边相等得到AD=AE,再根据斜边直角边定理证明△ADO和△AEO全等,然后利用全等三角对应角相等即可证明AO平分∠BAC.
解答:解:能实现.
理由:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠AEB=∠ADC=90°,
在△ABE和△ACD中,
,
∴AD=AE,
在Rt△ADO和Rt△AEO中,
,
∴Rt△ADO≌Rt△AEO(HL),
∴∠DAO=∠EAO,
∴AO平分∠BAC.
理由:∵CD⊥AB于点D,BE⊥AC于点E,
∴∠AEB=∠ADC=90°,
在△ABE和△ACD中,
|
∴AD=AE,
在Rt△ADO和Rt△AEO中,
|
∴Rt△ADO≌Rt△AEO(HL),
∴∠DAO=∠EAO,
∴AO平分∠BAC.
点评:本题考查了三角形全等的判定及性质;本题两次证明三角形全等和全等三角形的性质,熟练掌握判定定理和性质是解题的关键.

练习册系列答案
相关题目
小明设计了一个关于实数运算的程序:输出的数比该数的平方小1,小刚按此程序输入2
后,输出的结果应为( )
| 3 |
| A、10 | B、11 | C、12 | D、13 |
 在一次数学活动中,爱动脑筋的小华同学设计了一个几何模型:将一个面积为1的正方形按照图示进行分割.研究发现,图中蕴含着一个美妙的数量关系.
在一次数学活动中,爱动脑筋的小华同学设计了一个几何模型:将一个面积为1的正方形按照图示进行分割.研究发现,图中蕴含着一个美妙的数量关系.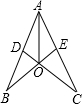 小刚设计了一个玩具模型,如图所示,其中AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD、BE相交于点O,为了使图形美观,小刚希望AO恰好平分∠BAC,他的这个愿望能实现吗?请你帮他说明理由.
小刚设计了一个玩具模型,如图所示,其中AB=AC,CD⊥AB于点D,BE⊥AC于点E,CD、BE相交于点O,为了使图形美观,小刚希望AO恰好平分∠BAC,他的这个愿望能实现吗?请你帮他说明理由.