题目内容
 如图,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,BC=DC,过点C作CE⊥AD的延长线于点E.
如图,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O上,BC=DC,过点C作CE⊥AD的延长线于点E.(1)求证:CE是⊙O的切线;
(2)若AB=10,AC=8,求tan∠DCE的值.
分析:(1)连接OC,OA=OC,则∠OCA=∠OAC,再由已知条件,可得∠ODE=90°;
(2)由CE是⊙O的切线,得∠DCE=∠CAE=∠CAB,从而求得tan∠DCE的值.
(2)由CE是⊙O的切线,得∠DCE=∠CAE=∠CAB,从而求得tan∠DCE的值.
解答: 解:(1)连接OC,
解:(1)连接OC,
∵OA=OC,
∴∠OCA=∠OAC,
∵DC=BC,
∴∠BAC=∠CAD,
∴∠OCA=∠CAD,
∵∠CAD+∠ACE=90°,∠ACE+∠ACO=90°,
∴OC⊥CE,
∴CE是⊙O的切线;
(2)∵CE是⊙O的切线,
∴∠DCE=∠CAE=∠CAB,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=10,AC=8,
∴BC=6,
∴tan∠DCE=tan∠BAC=
=
=
.
 解:(1)连接OC,
解:(1)连接OC,∵OA=OC,
∴∠OCA=∠OAC,
∵DC=BC,
∴∠BAC=∠CAD,
∴∠OCA=∠CAD,
∵∠CAD+∠ACE=90°,∠ACE+∠ACO=90°,
∴OC⊥CE,
∴CE是⊙O的切线;
(2)∵CE是⊙O的切线,
∴∠DCE=∠CAE=∠CAB,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=10,AC=8,
∴BC=6,
∴tan∠DCE=tan∠BAC=
| BC |
| AC |
| 6 |
| 8 |
| 3 |
| 4 |
点评:本题考查了切线的判定定理和勾股定理,三角函数的定义,通过此题可知三角函数值只与角的大小有关.都是基础知识要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD=
15、如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4.BD为⊙O的直径,则BD= 21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.
21、如图,△ABC内接于⊙O,AB为⊙O的直径,点D在AB的延长线上,∠A=∠D=30°.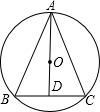 已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积.
已知:如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若AO=5,BC=8,∠ADB=90°,求△ABC的面积. 18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( )
18、如图,△ABC内接于⊙O,∠A=30°,若BC=4cm,则⊙O的直径为( ) 如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.
如图,△ABC内接于⊙O,AD⊥BC于点D,求证:∠BAD=∠CAO.