题目内容
12.如果一个正多边形的每个外角为72°,那么这个正多边形的边数为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 正多边形的外角和是360°,这个正多边形的每个外角相等,因而用360°除以外角的个数,就得到外角和中外角的个数,外角的个数就是多边形的边数.
解答 解:∵多边形的外角和为360°,
∴边数=360°÷72°=5,
故这个正多边形的边数是5.
故选:A.
点评 考查了多边形内角与外角,根据正多边形的外角和求多边形的边数是常用的一种方法,需要熟记.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
2.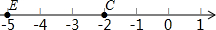 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )
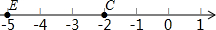 如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )
如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动多少次后该点到原点的距离不小于41( )| A. | 26 | B. | 27 | C. | 28 | D. | 29 |
20. 某篮球队12名队员的年龄统计如图所示,则该队队员年龄的众数和中位数分别是( )
某篮球队12名队员的年龄统计如图所示,则该队队员年龄的众数和中位数分别是( )
 某篮球队12名队员的年龄统计如图所示,则该队队员年龄的众数和中位数分别是( )
某篮球队12名队员的年龄统计如图所示,则该队队员年龄的众数和中位数分别是( )| A. | 16,15 | B. | 15,15.5 | C. | 15,17 | D. | 15,16 |
17.一组数据1,0,-1,2,3的中位数是( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
18.将13465000元,用科学记数法表示(保留3个有效数字)( )
| A. | 1.35×107 | B. | 1.34×107 | C. | 1.30×107 | D. | 0.135×108 |
19.下列等式正确的是( )
| A. | -$\sqrt{25}$=-5 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | $\sqrt{16}$=±4 | D. | -$\root{3}{-8}$=-2 |
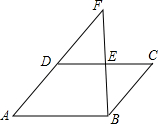 如图,E是?ABCD的边CD的中点,AD,BE的延长线交于点F,已知CE=2,?ABCD的周长等于14,则DF的长为( )
如图,E是?ABCD的边CD的中点,AD,BE的延长线交于点F,已知CE=2,?ABCD的周长等于14,则DF的长为( )