题目内容
【题目】问题背景：在
中，
、
、
三边的长分别为
、
、
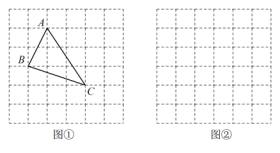
，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为 
），在网格中画出格点 （即 三个顶点都在小正方形的顶点处），如图所示，这样借用网格就能计算出它的面积．
（1）请你直接写出 的面积为 ．
（2）若三边的长分别为
、
、
运用构图法求出这三角形的面积．
【答案】（1）
;（2） 
【解析】
（1）利用恰好能覆盖△ABC的边长为3的小正方形的面积减去三个小直角三角形的面积即可解答；
（2）结合（1）易得此三角形的三边分别是直角边长为m，4n的直角三角形的斜边；直角边长为3m，2n的直角三角形的斜边；直角边长为2m，2n的直角三角形的斜边．进而得出面积.
解：（1）如图，
S△ABC=3×3-
×3×1-×2×1-×3×2=3.5；
（2）构造△ABC所示，
S△ABC=3m×4n-×m×4n-×3m×2n-×2m×2n=5mn．
练习册系列答案
相关题目
