题目内容
如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O2经过⊙O1的圆心O1,两圆的连心线交⊙O1于点M,交AB于点N,连结BM,已知AB=2 。
。
(1)求证:BM是⊙O2的切线;
(2)求 的长。
的长。
 。
。(1)求证:BM是⊙O2的切线;
(2)求
 的长。
的长。 
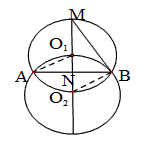
解:如图,连结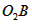 , ,∵⊙O1和⊙O2是等圆,且O1在⊙O2上, ∴点O2也在⊙O1上, ∵O1O2是两圆的连心线, ∴MO2是⊙O1的直径, ∴∠MBO2=90°, 又∵直线BM经过半径的O2B的外端, ∴直线BM是⊙O2的切线; |
 |
| (2)连结O1A、O1B, ∵点B既在⊙O1上,又在⊙O2上, ∴O1O2=O1B=O2B, ∴∠NO1B=60°, ∵O1O2是两圆的连心线, ∴O1O2⊥AB,BN= 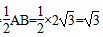 , ,在Rt△NO1B中,sin60°= 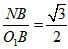 ,O1B=2, ,O1B=2,∵O1M=O1B, ∴∠O1MB =∠O1BM= 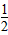 ∠BO1N = ∠BO1N =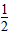 ×60°=30°, ×60°=30°,∴在Rt△MBN中,∠MBN= 60°, ∴∠MO1A=120°, ∴ 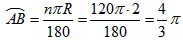 。 。 |

练习册系列答案
相关题目
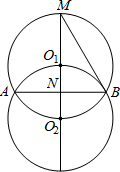 于点N,连接BM,已知AB=2
于点N,连接BM,已知AB=2
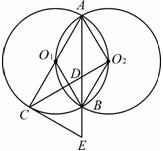
 (2012•桂林)如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.
(2012•桂林)如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心,顺次连接A、O1、B、O2.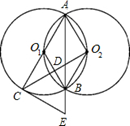
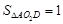 ,求
,求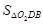 的值.
的值.