Question

等边三角形的边长为4，则此三角形内切圆的半径为________．

Answer 1

分析：根据等边三角形的性质连接AD、BO得出AD过O，推出OD⊥BC，∠OBD=30°，BD=BC=2，推出OB=2OD，设OD=a，得出OB=2a，在Rt△ODB中由勾股定理得出关于a的方程，求出方程的解即可．
解答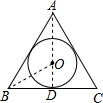：等边△ABC的内切圆O切BC于D，连接AD，则AD过O，连接BO，
∵⊙O是等边△ABC的内切圆，
∴OD⊥BC，∠OBD=×60°=30°，BD=DC=BC=2，
∴OD=OB，
设OD=a，则OB=2a，
在Rt△ODB中，由勾股定理得：OB²=BD²+OD²，
即（2a）²=2²+a²，
解得：a=．
故答案为：．
点评：本题考查了等边三角形的性质，三角形的内切圆，勾股定理等知识点的应用，关键是构造直角三角形，主要培养了学生运用定理进行计算的能力，用的数学思想是方程思想．