��Ŀ����
��ͼ����֪������y1=-2x2+2��ֱ��y2=2x+2����x��ȡһֵʱ��x��Ӧ�ĺ���ֵ�ֱ�Ϊy1��y2����y1��y2��ȡy1��y2�еĽ�Сֵ��ΪM����y1=y2����M=y1=y2�����磺��x=1ʱ��y1=0��y2=4��y1��y2����ʱM=0�������жϣ��ٵ�x��0ʱ��y1��y2�� �ڵ�x��0ʱ��xֵԽ��MֵԽС��
��ʹ��M����2��xֵ�����ڣ� ��ʹ��M=1��xֵ��
 ��
�� ��
��������ȷ���ǣ� ��

A���٢�
B���٢�
C���ڢ�
D���ۢ�
���𰸡�����������ͼ���������ύ���Լ�Mֵ��ȡ�����ֱ�����ͼ����з������ɵó��𰸣�
����⣺�ߵ�x��0ʱ�����ú���ͼ����Եó�y2��y1����ٴ���
��������y1=-2x2+2��ֱ��y2=2x+2����x��ȡһֵʱ��x��Ӧ�ĺ���ֵ�ֱ�Ϊy1��y2����y1��y2��ȡy1��y2�еĽ�Сֵ��ΪM��
�൱x��0ʱ�����ݺ���ͼ����Եó�xֵԽ��MֵԽ��ڴ���
��������y1=-2x2+2��ֱ��y2=2x+2����y�ύ������Ϊ����0��2������x=0ʱ��M=2��������y1=-2x2+2�����ֵΪ2����M����2��xֵ�����ڣ�
��ʹ��M����2��xֵ�����ڣ������ȷ��
�ߵ�-1��x��0ʱ��
ʹ��M=1ʱ��������y1=-2x2+2=1����ã�x1= ��x2=-
��x2=- ��
��
��y2=2x+2=1����ã�x=- ��
��
��ͼ��ɵó�����x= ��0����ʱ��Ӧy1=M��
��0����ʱ��Ӧy1=M��
��������y1=-2x2+2��x�ύ������Ϊ����1��0������-1��0����
�൱-1��x��0����ʱ��Ӧy2=M��
��M=1ʱ��x1= ��x2=-
��x2=- ��
��
ʹ��M=1��xֵ�� ��
�� �������ȷ��
�������ȷ��
����ȷ���У��ۢܣ�
��ѡ��D��
������������Ҫ�����˶��κ�����һ�κ����ۺ�Ӧ�ã��������ν�ϵó������������ǽ���ؼ���
����⣺�ߵ�x��0ʱ�����ú���ͼ����Եó�y2��y1����ٴ���
��������y1=-2x2+2��ֱ��y2=2x+2����x��ȡһֵʱ��x��Ӧ�ĺ���ֵ�ֱ�Ϊy1��y2����y1��y2��ȡy1��y2�еĽ�Сֵ��ΪM��
�൱x��0ʱ�����ݺ���ͼ����Եó�xֵԽ��MֵԽ��ڴ���
��������y1=-2x2+2��ֱ��y2=2x+2����y�ύ������Ϊ����0��2������x=0ʱ��M=2��������y1=-2x2+2�����ֵΪ2����M����2��xֵ�����ڣ�
��ʹ��M����2��xֵ�����ڣ������ȷ��
�ߵ�-1��x��0ʱ��
ʹ��M=1ʱ��������y1=-2x2+2=1����ã�x1=
 ��x2=-
��x2=- ��
����y2=2x+2=1����ã�x=-
 ��
����ͼ��ɵó�����x=
 ��0����ʱ��Ӧy1=M��
��0����ʱ��Ӧy1=M����������y1=-2x2+2��x�ύ������Ϊ����1��0������-1��0����
�൱-1��x��0����ʱ��Ӧy2=M��
��M=1ʱ��x1=
 ��x2=-
��x2=- ��
��ʹ��M=1��xֵ��
 ��
�� �������ȷ��
�������ȷ������ȷ���У��ۢܣ�
��ѡ��D��
������������Ҫ�����˶��κ�����һ�κ����ۺ�Ӧ�ã��������ν�ϵó������������ǽ���ؼ���

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
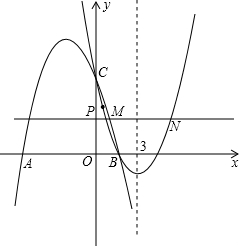
 ��2012•�����У���ͼ����֪������y1=-2x2+2��ֱ��y2=2x+2����x��ȡһֵʱ��x��Ӧ�ĺ���ֵ�ֱ�Ϊy1��y2����y1��y2��ȡy1��y2�еĽ�Сֵ��ΪM����y1=y2����M=y1=y2�����磺��x=1ʱ��y1=0��y2=4��y1��y2����ʱM=0�������жϣ�
��2012•�����У���ͼ����֪������y1=-2x2+2��ֱ��y2=2x+2����x��ȡһֵʱ��x��Ӧ�ĺ���ֵ�ֱ�Ϊy1��y2����y1��y2��ȡy1��y2�еĽ�Сֵ��ΪM����y1=y2����M=y1=y2�����磺��x=1ʱ��y1=0��y2=4��y1��y2����ʱM=0�������жϣ�
 ��ͼ����֪������
��ͼ����֪������