题目内容
 如图,四边形ADEF为菱形,且AB=14cm,BC=12cm,AC=10cm,那么BE=
如图,四边形ADEF为菱形,且AB=14cm,BC=12cm,AC=10cm,那么BE=考点:菱形的性质,相似三角形的判定与性质
专题:
分析:由已知可得△BDE∽△BAC,从而得到BD:AB=DE:AC,根据已知不难求得菱形的边长,再根据相似三角形的性质求得BE的长.
解答:解:∵四边形ADEF为菱形,
∴DE∥AC,AD=DE,
∴△BDE∽△BAC,
∴BD:AB=DE:AC,
∵AB=14cm,AC=10cm,
∴(14-DE):14=DE:10,
解得DE=
cm,
∴BE:BC=DE:AC,
即BE:12=
:10,
解得BE=7cm.
故答案为:7.
∴DE∥AC,AD=DE,
∴△BDE∽△BAC,
∴BD:AB=DE:AC,
∵AB=14cm,AC=10cm,
∴(14-DE):14=DE:10,
解得DE=
| 35 |
| 6 |
∴BE:BC=DE:AC,
即BE:12=
| 35 |
| 6 |
解得BE=7cm.
故答案为:7.
点评:此题主要考查菱形的性质:①菱形具有平行四边形的一切性质;②菱形的四条边都相等.同时考查了相似三角形的性质.

练习册系列答案
相关题目
若2是关于方程x2-5x+c=0的一个根,则这个方程的另一个根是( )
| A、-3 | B、3 | C、-6 | D、6 |
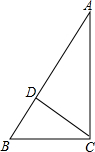 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,BC=3,AC=4,求AB、CD的长.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,BC=3,AC=4,求AB、CD的长.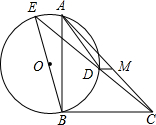 如图,BE是⊙O的直径,∠BAD=∠BCD,AB=5,BC=6,M为AC的中点.则DM=
如图,BE是⊙O的直径,∠BAD=∠BCD,AB=5,BC=6,M为AC的中点.则DM=