题目内容
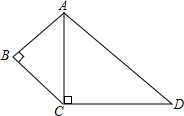 如图,AC平分∠BAD,AB⊥BC,CA⊥CD,AC=CD,AB=3,则AD=________.
如图,AC平分∠BAD,AB⊥BC,CA⊥CD,AC=CD,AB=3,则AD=________.
6
分析:由AC=CD,且CA与CD垂直,得到三角形ACD为等腰直角三角形,可得出∠CAD=45°,由AC平分∠BAD,得到∠BAC=∠CAD=45°,再由AB与BC垂直,得到三角形ABC为等腰直角三角形,可得出AB=BC=3,利用勾股定理求出AC的长,即为CD的长,再利用勾股定理即可求出AD的长.
解答:∵AC=CD,CA⊥CD,
∴△ACD为等腰直角三角形,
∴∠CAD=45°,
∵AC平分∠BAD,
∴∠BAC=∠CAD=45°,
又AB⊥BC,∴∠B=90°,
∴△ABC为等腰直角三角形,
∴AB=BC=3,
根据勾股定理得:AC= =3
=3 ,
,
∴AC=CD=3 ,
,
根据勾股定理得:AD= =6.
=6.
故答案为:6
点评:此题考查了等腰直角三角形的判定与性质,勾股定理,以及角平分线定义,熟练掌握等腰直角三角形的判定与性质是解本题的关键.
分析:由AC=CD,且CA与CD垂直,得到三角形ACD为等腰直角三角形,可得出∠CAD=45°,由AC平分∠BAD,得到∠BAC=∠CAD=45°,再由AB与BC垂直,得到三角形ABC为等腰直角三角形,可得出AB=BC=3,利用勾股定理求出AC的长,即为CD的长,再利用勾股定理即可求出AD的长.
解答:∵AC=CD,CA⊥CD,
∴△ACD为等腰直角三角形,
∴∠CAD=45°,
∵AC平分∠BAD,
∴∠BAC=∠CAD=45°,
又AB⊥BC,∴∠B=90°,
∴△ABC为等腰直角三角形,
∴AB=BC=3,
根据勾股定理得:AC=
 =3
=3 ,
,∴AC=CD=3
 ,
,根据勾股定理得:AD=
 =6.
=6.故答案为:6
点评:此题考查了等腰直角三角形的判定与性质,勾股定理,以及角平分线定义,熟练掌握等腰直角三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
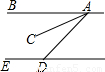
 (2012•铁岭)如图所示,BA∥ED,AC平分∠BAD,∠BAC=23°,则∠EDA的度数是
(2012•铁岭)如图所示,BA∥ED,AC平分∠BAD,∠BAC=23°,则∠EDA的度数是 如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )
如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )