Question

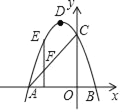
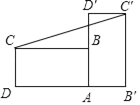
【题目】如图，把矩形ABCD绕点A顺时针旋转，使点B的对应点B落在DA的延长线上，若AB＝2，BC＝4，则点C与其对应点C的距离为( )

A. 6 B. 8 C. 2 D. 2

Answer 1

【答案】D

【解析】

连接AC、AC′，如图，由勾股定理得，AC＝2，再利用旋转的性质得到∠CAC′＝∠BAB′＝90°，AC＝AC′，则可判断△ACC′为等腰直角三角形，然后根据等腰直角三角形求CC′的长．

连接AC、AC′，如图，

∵四边形ABCD为矩形，

∴∠DAB＝∠ABC＝90°，

在Rt△ABC中，AC＝，

∵矩形ABCD绕点A顺时针旋转，使点B的对应点B落在DA的延长线上，

∴∠CAC′＝∠BAB′＝90°，AC＝AC′，

∴△ACC′为等腰直角三角形，

∴CC′＝．

故选D．