题目内容
 如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为9m,则旗杆的高度是多少?(结果保留根号)
如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为9m,则旗杆的高度是多少?(结果保留根号)
解:在Rt△ACD中,
∵tan∠ACD= ,
,
∴tan30°= ,
,
∴ =
= ,
,
∴AD=3 m,
m,
在Rt△BCD中,
∵tan∠BCD=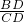 ,
,
∴tan45°= ,
,
∴BD=9m,
∴AB=AD+BD=3 +9(m).
+9(m).
答:旗杆的高度是(3 +9)m.
+9)m.
分析:根据在Rt△ACD中,tan∠ACD= ,求出AD的值,再根据在Rt△BCD中,tan∠BCD=
,求出AD的值,再根据在Rt△BCD中,tan∠BCD=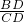 ,求出BD的值,最后根据AB=AD+BD,即可求出答案.
,求出BD的值,最后根据AB=AD+BD,即可求出答案.
点评:此题考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.
∵tan∠ACD=
 ,
,∴tan30°=
 ,
,∴
 =
= ,
,∴AD=3
 m,
m,在Rt△BCD中,
∵tan∠BCD=
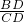 ,
,∴tan45°=
 ,
,∴BD=9m,
∴AB=AD+BD=3
 +9(m).
+9(m).答:旗杆的高度是(3
 +9)m.
+9)m.分析:根据在Rt△ACD中,tan∠ACD=
 ,求出AD的值,再根据在Rt△BCD中,tan∠BCD=
,求出AD的值,再根据在Rt△BCD中,tan∠BCD=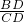 ,求出BD的值,最后根据AB=AD+BD,即可求出答案.
,求出BD的值,最后根据AB=AD+BD,即可求出答案.点评:此题考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
相关题目
 (2013•襄阳)如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为9m,则旗杆的高度是多少?(结果保留根号)
(2013•襄阳)如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为9m,则旗杆的高度是多少?(结果保留根号)
 如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为9m,则旗杆的高度是多少?(结果保留根号)
如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为9m,则旗杆的高度是多少?(结果保留根号)