题目内容
（2013•襄阳）如图，在数学活动课中，小敏为了测量校园内旗杆AB的高度，站在教学楼上的C处测得旗杆低端B的俯角为45°，测得旗杆顶端A的仰角为30°，如旗杆与教学楼的水平距离CD为9m，则旗杆的高度是多少？（结果保留根号）分析：根据在Rt△ACD中，tan∠ACD=
，求出AD的值，再根据在Rt△BCD中，tan∠BCD=
，求出BD的值，最后根据AB=AD+BD，即可求出答案．
| AD |
| DC |
| BD |
| CD |
解答：解：在Rt△ACD中，
∵tan∠ACD=
，
∴tan30°=
，
∴
=
，
∴AD=3
m，
在Rt△BCD中，
∵tan∠BCD=
，
∴tan45°=
，
∴BD=9m，
∴AB=AD+BD=3
+9（m）．
答：旗杆的高度是（3
+9）m．
∵tan∠ACD=
| AD |
| DC |
∴tan30°=
| AD |
| 9 |
∴
| AD |
| 9 |
| ||
| 3 |
∴AD=3
| 3 |
在Rt△BCD中，
∵tan∠BCD=
| BD |
| CD |
∴tan45°=
| BD |
| 9 |
∴BD=9m，
∴AB=AD+BD=3
| 3 |
答：旗杆的高度是（3
| 3 |
点评：此题考查了解直角三角形的应用-仰角俯角问题，本题要求学生借助俯角构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2013•襄阳）如图，BD平分∠ABC，CD∥AB，若∠BCD=70°，则∠ABD的度数为（ ）
（2013•襄阳）如图，平行四边形ABCD的对角线交于点O，且AB=5，△OCD的周长为23，则平行四边形ABCD的两条对角线的和是（ ）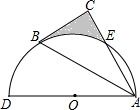
（2013•襄阳）如图，以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点，交直角边AC于点E，B、E是半圆弧的三等分点，弧BE的长为
（2013•襄阳）如图，水平放置的圆柱形排水管道的截面直径是1m，其中水面的宽AB为0.8m，则排水管内水的深度为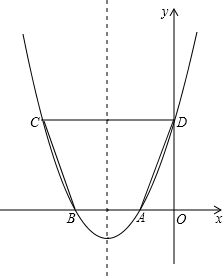
（2013•襄阳）如图，已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为（-1，0），对称轴为直线x=-2．