题目内容
在△ABC中，已知点D、E分别在边AB、AC上，如果AD=2cm，DB=4cm，AE=3cm，EC=1cm，DE=2.5cm，那么BC=分析：首先根据相似三角形的判定证明△ADE∽△ACB，再根据相似三角形的性质求解．
解答：解：∵AD=2cm，DB=4cm，AE=3cm，EC=1cm，
∴
=
=
，
=
=
，
∴
=
，
又∠A=∠A，
∴△ADE∽△ACB，
∴
=
，
则BC=5（cm）．
故答案为5．
∴
| AE |
| AB |
| 3 |
| 6 |
| 1 |
| 2 |
| AD |
| AC |
| 2 |
| 4 |
| 1 |
| 2 |
∴
| AE |
| AB |
| AD |
| AC |
又∠A=∠A，
∴△ADE∽△ACB，
∴
| DE |
| BC |
| 1 |
| 2 |
则BC=5（cm）．
故答案为5．
点评：此题综合运用了相似三角形的判定和性质．
相似三角形的判定：两个角对应相等的两个三角形相似；两条对应边的比相等，且夹角相等的两个三角形相似；三条对应边的比相等的两个三角形相似．
相似三角形的性质：相似三角形的对应角相等，对应边的比相等．
相似三角形的判定：两个角对应相等的两个三角形相似；两条对应边的比相等，且夹角相等的两个三角形相似；三条对应边的比相等的两个三角形相似．
相似三角形的性质：相似三角形的对应角相等，对应边的比相等．
练习册系列答案
阅读快车系列答案
相关题目
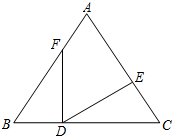如图，在△ABC中，已知点D、E、F分别在边BC、AC、AB上，且FD=ED，BF=CD，∠FDE=∠B，那么∠B和∠C的大小关系如何？为什么？
如图所示，在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC=4cm2，则S阴影等于（ ）| A、2cm2 | ||
| B、1cm2 | ||
C、
| ||
D、
|
如图，在△ABC中，已知点D，E，F分别为BC，AD，CE的中点，且
如图，在△ABC中，已知点A（0，3），B（-2，-3），C（3，-5）．