Question

【题目】如图，已知坐标平面上有一顶点为的抛物线，点坐标为，则可设此抛物线的顶点式为______；若此抛物线又与直线交于、两点，且为正三角形，则可求得此抛物线与轴的交点坐标为________________

Answer 1

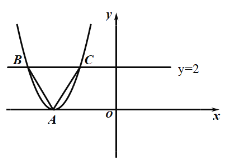
【答案】

【解析】

设B（-3-m，2），C（-3+m，2），（m＞0），可知BC=2m，再由等边三角形的性质可知C（-3+ ，2），设抛物线解析式y=a（x+3）2，将点C代入解析式即可求a，进而求解；

解：设B（-3-m，2），C（-3+m，2），（m＞0）
∵A点坐标为（-3，0），
∴BC=2m，
∵△ABC为正三角形，
∴AC=BC=2m，∠CAO=60°，
∴m=
∴C（-3+，2）
设抛物线解析式y=a（x+3）2，
a（-3++3）2=2，
∴a= ，
∴y=（x+3）2，
当x=0时，y=；
故答案为：，．