题目内容
6.已知点C为线段AB的黄金分割点(AC>BC),已知AB=10,则BC=15-5$\sqrt{5}$.分析 根据黄金分割点的定义,知AC为较长线段;则AC=$\frac{\sqrt{5}-1}{2}$AB,代入数据即可得出AC的值,然后计算AB-AC即可得到BC.
解答 解:∵C为线段AB的黄金分割点(AC>BC),
∴AC=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$×10=5$\sqrt{5}$-5,
∴BC=AB-AC=10-(5$\sqrt{5}$-5)=15-5$\sqrt{5}$.
故答案为:15-5$\sqrt{5}$
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
16.下列说法中错误的是( )
| A. | 0和x都是单项式 | B. | -$\frac{2x+y}{2}$与$\frac{1}{x}$都不是单项式 | ||
| C. | a2-3ab+2b3 是三次三项式 | D. | -2πx2y的系数是-2,次数是3 |
14. 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
 正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )
正方形ABCD在数轴上的位置如图所示,点D、A对应的数分别为0和1,若正方形ABCD绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为2;则翻转2016次后,数轴上数2016所对应的点是( )| A. | 点C | B. | 点D | C. | 点A | D. | 点B |
1.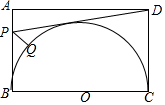 如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )
如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )
 如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )
如图,矩形ABCD中,AB=3,BC=4,P是边AB上一点,Q是以BC为直径的圆上一点,则DP+PQ的最小值为( )| A. | 5 | B. | $\sqrt{13}$+2 | C. | $\frac{\sqrt{73}}{2}$+$\frac{1}{2}$ | D. | 3$\sqrt{5}$-2 |
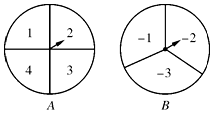 如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止.
如图,甲、乙两人在玩转盘游戏时,准备了两个可以自由转动的转盘A,B,每个转盘被分成面积相等的几个扇形,并在每一个扇形内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所指区域的数字之和为0时,甲获胜;数字之和为1时,乙获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止. 如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+12与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M.
如图,在平面直角坐标系中,一次函数y=-$\frac{3}{4}$x+12与两坐标轴分别交于A,B两点,OM⊥AB,垂足为点M. 如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,BE=CF,BF交CE于P,连PD,下列结论:①AC=AE,②CD=BE,③PB=PF,④DP=BF,其中正确的结论是( )
如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,BE=CF,BF交CE于P,连PD,下列结论:①AC=AE,②CD=BE,③PB=PF,④DP=BF,其中正确的结论是( ) 如图,在⊙O中,OA、OB是半径,OA⊥OB,C、D是$\widehat{AB}$的三等分点,OC、OD分别交AB于点E、F,求证:AE=CD=BF.
如图,在⊙O中,OA、OB是半径,OA⊥OB,C、D是$\widehat{AB}$的三等分点,OC、OD分别交AB于点E、F,求证:AE=CD=BF.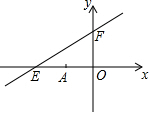 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.如图中的一次函数图象与x轴、y轴分别相交于点E,F,则△OEF为此函数的坐标三角形.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.如图中的一次函数图象与x轴、y轴分别相交于点E,F,则△OEF为此函数的坐标三角形.