题目内容
27、五边形ABCDE中，∠A为135°，AE⊥ED，AB∥CD，∠B=∠D，试求∠C的度数．
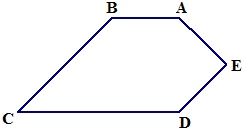
分析：先根据多边形内角和定理求出其内角和，根据∠A为135°，AE⊥DE，∠B=∠D可求出∠C+∠B+∠D的度数，再根据平行线的性质可得∠B+∠C=180°，把三式联立即可求出∠C的度数．
解答：解：∵此多边形是五边形，
∴其内角和为：（5-2）×180°=540°，
∵∠A为135°，AE⊥DE，∠B=∠D，
∴∠C+∠B+∠D=540°-135°-90°=315°…①，
∵AB∥CD，
∴∠B+∠C=180°…②，
∵∠B=∠D…③，
①②③联立得，∠C=45°．
故答案为：45°．
∴其内角和为：（5-2）×180°=540°，
∵∠A为135°，AE⊥DE，∠B=∠D，
∴∠C+∠B+∠D=540°-135°-90°=315°…①，
∵AB∥CD，
∴∠B+∠C=180°…②，
∵∠B=∠D…③，
①②③联立得，∠C=45°．
故答案为：45°．
点评：本题考查的是多边形的内角和定理及平行线的性质，先根据多边形内角和定理求出∠C+∠B+∠D的度数是解答此题的关键．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
如图，正五边形ABCDE中，DC和AB的延长线交于F，则图中与△DBF相似的三角形有（不再添加其他的线段和字母，不包括△DBF本身）（ ）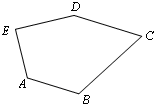
19、如图，在五边形ABCDE中，AE⊥DE，∠BAE=120°，∠BCD=60°，∠CDE-∠ABC=30°．
已知：如图，在正五边形ABCDE中，BE分别与AC、AD相交于F、G，下列说法不正确的是（ ）
如图，在五边形ABCDE中，AE⊥DE，垂足为E，∠D=150°，∠A=∠B，∠B-∠C=60°，则∠A的度数为（ ）
已知：如图，五边形ABCDE中，AB∥CD，求图形中∠AED的值．