��Ŀ����
��ͼ���ڱ߳���2��������ABCD�У���F��x����һ�㣬CF=1������B��BF��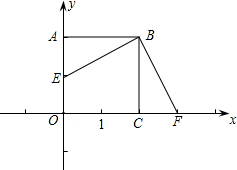 ���ߣ���y���ڵ�E��
���ߣ���y���ڵ�E����1�������E��B��F�������ߵĽ���ʽ��
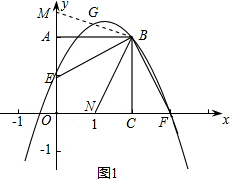
��2������EBF�Ƶ�B˳ʱ����ת���ǵ�һ�߽�y���������ڵ�M����һ�߽�x���ڵ�N����BM�루1���������ߵ���һ����ΪG������G�ĺ�����Ϊ
| 6 |
| 5 |
��3����P�ڣ�1���е��������ϣ���PE��y��������ǵ�����ֵΪ
| 3 |
| 2 |
��������1�����������εı߳������B��F�����꣮����EBF=90�㣬��ô��ABE����CBFΪͬ�ǵ���ǣ��ɴ˿�֤�á�ABE�ա�CBF���������AE�ij����Ӷ��ɵõ�E�����꣬�Ӷ����ô���ϵ������ø������ߵĽ���ʽ��
��2�����ݵ�G�ĺ����꣬��ȷ��G������꣬�����ֱ��BG�Ľ���ʽ���Ӷ��õ�M������꣬���ɵõ�EM��AM�ij����ɣ�1��֪AM=CN���ɴ˿����CN��ON�ij���Ȼ������EM��ON��������ϵ��
��3������Ӧ������������ǣ�
�ٵ���P��E���Ϸ�ʱ����P��PH��y����H������PE�����������ߵĽ���ʽ�������P�����꣬���ɵõ�EH��PH�ij���Ȼ����ݡ�PEH������ֵ�����P�����꣮
�ڵ���P��E���·�ʱ������ͬ�٣�
��2�����ݵ�G�ĺ����꣬��ȷ��G������꣬�����ֱ��BG�Ľ���ʽ���Ӷ��õ�M������꣬���ɵõ�EM��AM�ij����ɣ�1��֪AM=CN���ɴ˿����CN��ON�ij���Ȼ������EM��ON��������ϵ��
��3������Ӧ������������ǣ�
�ٵ���P��E���Ϸ�ʱ����P��PH��y����H������PE�����������ߵĽ���ʽ�������P�����꣬���ɵõ�EH��PH�ij���Ȼ����ݡ�PEH������ֵ�����P�����꣮
�ڵ���P��E���·�ʱ������ͬ�٣�
����⣺��1�������⣬�ɵõ�B��2��2����
��CF=1��
��F��3��0����
��������ABCD�У���ABC=��OAB=��BCF=90�㣬AB=BC��
��BE��BF��
���EBF=90�㣬
���EBF=��ABC��
����ABE+��EBC=��EBC+��CBF��
���ABE=��CBF��
���ABE�ա�CBF��
��E��0��1����
�����E��B��F�������ߵĽ���ʽΪy=ax2+bx+1�����У�
��
���
��
��������ߵĽ���ʽΪ��y=-
x2+
x+1��
��2����G��
��y)��������y=-
x2+
x+1����
��y=-
(
)2+
��
+1=
��
��G��
��
����
���B��G��ֱ�߽���ʽΪy=kx+b��
��
��
�����BE��ֱ�߽���ʽΪy=-
x+3��
��ֱ��y=-
x+3��y�ύ�ڵ�M��0��3����
��EM=2��
��֤��ABM�ա�CBN��
��CN=AM��
��ON=1��
��EM=2ON��
��3����P��������y=-
x2+
x+1�ϣ���P�������Ϊ��m��-
m2+
m+1)��
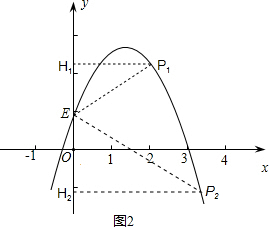 ��ͼ2���ٹ���P1��P1H1��y���ڵ�H1������P1E��
��ͼ2���ٹ���P1��P1H1��y���ڵ�H1������P1E��
��tan��H1EP1=
��
��
=
��
��
=
��
���m1=
��m2=0���������⣬��ȥ����
�ڹ���P2��P2H2��y���ڵ�H2������P2E��
��tan��H2EP2=
��
��
=
��
���m3=
��m4=0���������⣬��ȥ��
��m1=
ʱΪ
��
��m3=
ʱΪ-
��
������������P1��
��
����P2��
��-
������
��CF=1��
��F��3��0����
��������ABCD�У���ABC=��OAB=��BCF=90�㣬AB=BC��
��BE��BF��
���EBF=90�㣬
���EBF=��ABC��
����ABE+��EBC=��EBC+��CBF��
���ABE=��CBF��
���ABE�ա�CBF��
��E��0��1����
�����E��B��F�������ߵĽ���ʽΪy=ax2+bx+1�����У�
|
���
|
��������ߵĽ���ʽΪ��y=-
| 5 |
| 6 |
| 13 |
| 6 |
��2����G��
| 6 |
| 5 |
| 5 |
| 6 |
| 13 |
| 6 |
��y=-
| 5 |
| 6 |
| 6 |
| 5 |
| 13 |
| 6 |
| 6 |
| 5 |
| 16 |
| 5 |
��G��
| 6 |
| 5 |
| 12 |
| 5 |
���B��G��ֱ�߽���ʽΪy=kx+b��
��
|
��
|
�����BE��ֱ�߽���ʽΪy=-
| 1 |
| 2 |
��ֱ��y=-
| 1 |
| 2 |
��EM=2��
��֤��ABM�ա�CBN��
��CN=AM��
��ON=1��
��EM=2ON��

��3����P��������y=-
| 5 |
| 6 |
| 13 |
| 6 |
| 5 |
| 6 |
| 13 |
| 6 |
 ��ͼ2���ٹ���P1��P1H1��y���ڵ�H1������P1E��
��ͼ2���ٹ���P1��P1H1��y���ڵ�H1������P1E����tan��H1EP1=
| 3 |
| 2 |
��
| P1H1 |
| H1E |
| 3 |
| 2 |
��
| m | ||||
-
|
| 3 |
| 2 |
���m1=
| 9 |
| 5 |
�ڹ���P2��P2H2��y���ڵ�H2������P2E��
��tan��H2EP2=
| 3 |
| 2 |
��
| P2H2 |
| H2E |
| 3 |
| 2 |
���m3=
| 17 |
| 5 |
��m1=
| 9 |
| 5 |
| 11 |
| 5 |
��m3=
| 17 |
| 5 |
| 19 |
| 15 |
������������P1��
| 9 |
| 5 |
| 11 |
| 5 |
| 17 |
| 5 |
| 19 |
| 15 |
���������⿼���������ε����ʡ�ȫ�������ε��ж������ʡ����κ�������ʽ��ȷ����������Ǻ����Ķ����֪ʶ��ͬʱ�������˷������۵���ѧ˼�룬�ѶȽϴ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��֪����ͼ���ڱ߳�Ϊa������ABC�У��ֱ���A��B��C��ΪԲ�ģ�
��֪����ͼ���ڱ߳�Ϊa������ABC�У��ֱ���A��B��C��ΪԲ�ģ�
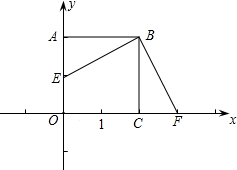 ���ߣ���y���ڵ�E��
���ߣ���y���ڵ�E�� ʱ��EM��NO��������������ϵ����˵����Ľ��ۣ�
ʱ��EM��NO��������������ϵ����˵����Ľ��ۣ� �����P�����꣮
�����P�����꣮ ʱ��EM��NO��������������ϵ����˵����Ľ��ۣ�
ʱ��EM��NO��������������ϵ����˵����Ľ��ۣ� �����P�����꣮
�����P�����꣮
 ��֪����ͼ���ڱ߳�Ϊa������ABC�У��ֱ���A��B��C��ΪԲ�ģ�
��֪����ͼ���ڱ߳�Ϊa������ABC�У��ֱ���A��B��C��ΪԲ�ģ� ��Ϊ�뾶��
��Ϊ�뾶�� ��
�� ��
�� ������Ӱ���ֵ������
������Ӱ���ֵ������