题目内容
如图，在△OAB中，O为坐标原点，横、纵轴的单位长度相同，A、B的坐标分别为(8，6)，(16，0)，点P沿OA边从点O开始向终点A运动，速度每秒1个单位，点Q沿BO边从B点开始向终点O运动，速度每秒2个单位，如果P、Q同时出发，用t(秒)表示移动时间，当这两点中有一点到达自己的终点时，另一点也停止运动。
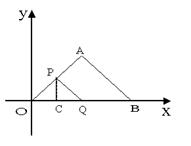
求(1)几秒时PQ∥AB
(2)设△OPQ的面积为y，求y与t的函数关系式
(3)△OPQ与△OAB能否相似，若能，求出点P的坐标，若不能，试说明理由
求(1)几秒时PQ∥AB
(2)设△OPQ的面积为y，求y与t的函数关系式
(3)△OPQ与△OAB能否相似，若能，求出点P的坐标，若不能，试说明理由
（1）40/9(2) 
(3) （
，
）
(3) （， ）（1）
，
，则：
，得：t=40/9
(2) 过P作PC⊥OB, 垂足为C, 过A作AD⊥OB, 垂足为D
(3)能相似。PQ∥AB, △OPQ∽△OAB
∵t=
∴OP= ,
∵
其中AD=6,OA=10,OD=8 ∴OC=,PC=,
∴P点坐标是（， ）.
（1）由两点间的距离公式求得AO=10，然后根据平行线PQ∥AB分线段成比例知，据此列出关于t的方程，并解方程；
（2）过P作PC⊥OB，垂足为C，过A作AD⊥OB，垂足为D．构造平行线PC∥AQ，根据平行线分线段成比例及三角形的面积公式求得关于y与t的函数关系式；
（3）当PQ∥AB时，得到两对同位角相等，利用两对对应角相等的两三角形相似可得△OPQ∽△OAB．然后根据相似三角形的性质：对应线段成比例求得点P的坐标
，，则：，得：t=40/9(2) 过P作PC⊥OB, 垂足为C, 过A作AD⊥OB, 垂足为D
(3)能相似。PQ∥AB, △OPQ∽△OAB
∵t=
∴OP= , ∵
其中AD=6,OA=10,OD=8 ∴OC=,PC=,∴P点坐标是（
， ）.（1）由两点间的距离公式求得AO=10，然后根据平行线PQ∥AB分线段成比例知
，据此列出关于t的方程，并解方程；（2）过P作PC⊥OB，垂足为C，过A作AD⊥OB，垂足为D．构造平行线PC∥AQ，根据平行线分线段成比例及三角形的面积公式求得关于y与t的函数关系式；
（3）当PQ∥AB时，得到两对同位角相等，利用两对对应角相等的两三角形相似可得△OPQ∽△OAB．然后根据相似三角形的性质：对应线段成比例求得点P的坐标
练习册系列答案
相关题目
，点E、F分别是线段AD、AC上的动点（点E不与点A、D重合），且∠CEF=∠ACB.
，求AD的长。（结果保留根号）
是
的中位线，则
与
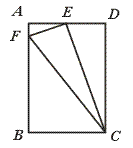
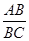＝k，是否存在这样的k值，使得△AEF与△BFC相似，若存在，证明你的结论并求出k的值；若不存在，说明理由．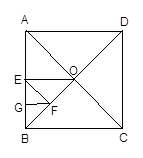
，则
。