题目内容
 如图,等腰△ABC的顶角∠A=40°,以AB为直径的半圆与BC、AC分别交于D、E两点,则∠EBC=________,
如图,等腰△ABC的顶角∠A=40°,以AB为直径的半圆与BC、AC分别交于D、E两点,则∠EBC=________, 的度数为________.
的度数为________.
20° 100°
分析:连AD,根据圆周角定理的推论得到∠ADB=90°,即AD⊥BC,又根据等腰三角形的性质得到AD平分∠BAC,得到∠BAD=∠DAC=20°,根据圆周角定理得∠EBC=∠DAC=20°;再根据圆周角的度数等于它所对的弧的度数的一半得到弧BD的度数=弧DE的度数=2×20°=40°,即可求出弧AE的度数.
解答:连AD,如图,
∵AB为直径,
∴∠ADB=90°,即AD⊥BC,
又∵AB=AC,
∴AD平分∠BAC,
而∠A=40°,
∴∠BAD=∠DAC=20°,
∴∠EBC=∠DAC=20°,
∴弧BD的度数=弧DE的度数=2×20°=40°,
∴弧AE的度数=180°-40°-40°=100°.
故答案为20°,100°.
点评:本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.也考查了圆周角定理及其推论、圆周角的度数等于它所对的弧的度数的一半以及等腰三角形的性质.
分析:连AD,根据圆周角定理的推论得到∠ADB=90°,即AD⊥BC,又根据等腰三角形的性质得到AD平分∠BAC,得到∠BAD=∠DAC=20°,根据圆周角定理得∠EBC=∠DAC=20°;再根据圆周角的度数等于它所对的弧的度数的一半得到弧BD的度数=弧DE的度数=2×20°=40°,即可求出弧AE的度数.
解答:连AD,如图,

∵AB为直径,
∴∠ADB=90°,即AD⊥BC,
又∵AB=AC,
∴AD平分∠BAC,
而∠A=40°,
∴∠BAD=∠DAC=20°,
∴∠EBC=∠DAC=20°,
∴弧BD的度数=弧DE的度数=2×20°=40°,
∴弧AE的度数=180°-40°-40°=100°.
故答案为20°,100°.
点评:本题考查了在同圆或等圆中,如果两个圆心角以及它们对应的两条弧、两条弦中有一组量相等,则另外两组量也对应相等.也考查了圆周角定理及其推论、圆周角的度数等于它所对的弧的度数的一半以及等腰三角形的性质.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 已知:如图,等腰△ABC的腰长为2
已知:如图,等腰△ABC的腰长为2 如图,等腰△ABC的底边BC为16,底边上的高AD为6,则腰长AB的长为
如图,等腰△ABC的底边BC为16,底边上的高AD为6,则腰长AB的长为 如图,等腰△ABC的腰长是5cm,底边长是6cm,P是底边BC上任意一点,PD⊥AB,PE⊥AC,垂足分别是D,E,那么PD+PE=
如图,等腰△ABC的腰长是5cm,底边长是6cm,P是底边BC上任意一点,PD⊥AB,PE⊥AC,垂足分别是D,E,那么PD+PE=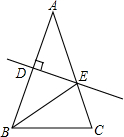 如图,等腰△ABC的周长为27,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
如图,等腰△ABC的周长为27,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( ) 如图,等腰△ABC的顶角为120°,腰长为10,则底边BC上的中线AD长为
如图,等腰△ABC的顶角为120°,腰长为10,则底边BC上的中线AD长为