题目内容
如图,CD切⊙O于B,CO的延长线交⊙O于A,若∠C=36°,则∠ABD的度数是( )


A.72° B.63° C.54° D.36°
B【考点】切线的性质;圆周角定理.
【分析】连接BE,根据CD切⊙O于B,由弦切角定理知,∠CBE=∠A,利用直径所对的角是直角可得∠AEB=90°﹣∠A=∠EBC+∠C=∠A+36°,从而求得∠ABD=∠AEB=90°﹣27°=63°.
【解答】解:连接BE,
∵CD切⊙O于B,
∴∠CBE=∠A,
∵∠AEB=90°﹣∠A=∠EBC+∠C=∠A+36°,
∴∠A=27°,
∴∠ABD=∠AEB=90°﹣27°=63°.
故选B.


【点评】本题利用了弦切角定理,直径对的圆周角是直角,三角形的外角与内角的关系即可求解.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( ) ×(﹣
×(﹣ )+|﹣2
)+|﹣2 |+(
|+(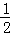 )﹣3.
)﹣3.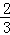 ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.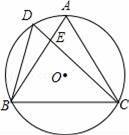

 ,则该三角形的周长为( )
,则该三角形的周长为( )